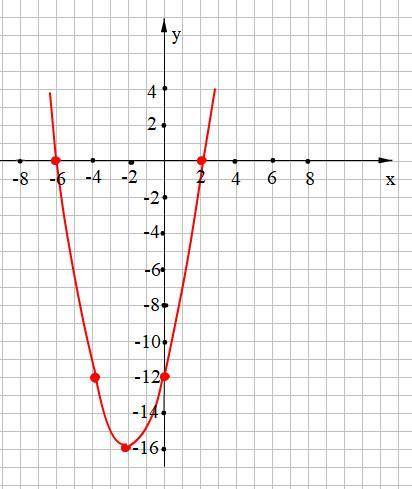
Функция у = х² + 4х - 12
График функции - квадратная парабола веточками вверх
Найдём характерные точки этой параболы.
1) Точка пересечения с осью Оу: х = 0; у = -12;
2) точки пересечения с осью Ох: у = 0
х² + 4х - 12 = 0
D = 4² - 4 · (-12) = 64
√D = 8
x₁ = (-4 - 8)/2 = -6
x₂ = (-4 + 8) = 2
Получили две точки (-6; 0) и (2; 0)
3) найдём координаты вершины С параболы С(m; n)
m = - b/2a = -4/2 = -2
n = y(-2) = (-2)² + 4 · (-2) - 12 = -16
C(-2; -16)
По найденным точкам строим параболу (смотри прикреплённый рисунок).
По графику находим
а) у > 0 при х ∈ (-∞; -6)∪(2; +∞); y < 0 при х ∈ (-6; 2)
б) у↑ при х ∈ (-2; +∞); у↓ при х ∈ (-∞; -2)
в) у наим = у(-2) = -16; наибольшего значения не существует.
опытаемся найти точки их пересечения, решив систему:
(x-2) 2 + (y-3) 2=16
(x-2) 2 + (y-2) 2=4
(x-2) 2=16 - (y-3) 2
(x-2) 2=4 - (y-2) 2,
отсюда 16 - (y-3) 2=4 - (y-2) 2
16-у2+6 у-9=4-у2+4 у-4 ещё
6 у-4 у=4-4+9-16 ещё
2 у=-7 найдём игрек
у=-3,5 и попробуем найти икс
(x-2) 2=4 - (-3,5-2) 2
(x-2) 2=4-30,25
(x-2) 2=-25,75, а квадрат не может быть отрицательным, следовательно, эти две окружности не пересекаются. центры окружностей - в точках (2; 3) и (2; 2) соответственно, то есть расстояние между центрами равно единице, а радиусы - 4 и 2, то есть вторая, меньшая, окружность расположена внутри первой.
ответ: малая окружность расположена внутри большой.
3x²=15
x²=5
x₁=√5 x₂=-√5
x₁+x₂=√5+(-√5)=0
ответ: 0