Изначально нужно сделать выбор 4 из 16 учеников без учета порядка, так как в конченом итоге они все окажутся в команде.
Теперь рассмотрим пожелания и внесем коррективы в этот выбор.
1) "Хулигана Васю брать точно нельзя"
Это означает, что выбирать мы теперь будем не из 16, а из 15 человек.
2) "Лучший геометр в параллели - Петя - однозначно будет в команде"
Это означает, что нам нужно выбрать не 4, а 3 человек, а также выбирать мы будем не из 15, а из 14 человек.
3) "А близняшек Аню и Таню нельзя разлучать ни в коем случае"
Рассмотрим две ситуации.
Первая ситуация. Аня и Таня попали в команду. Тогда, так как в команде точно есть еще и Петя, в ней осталось всего одно свободное место. Незадействованных учеников осталось 12 и любого из них можно добрать в команду. Таким образом, в этом случае мы имеем 12 вариантов.
Вторая ситуация. Аня и Таня не попали в команду. Тогда, в команде есть три свободных места, которые нужно заполнить, выбирая из оставшихся 12 учеников. Чтобы определить число это сделать, нужно посчитать число сочетаний из 12 по 3:
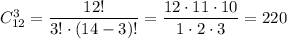
Таким образом, в этом случае мы имеем 220 вариантов.
Но так как первая и вторая ситуация несовместны (Аня и Таня не могут одновременно быть и не быть в команде), то полученные количества вариантов нужно сложить. Итого, число собрать команду:
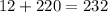
ответ
Объяснение:
По формулам sin 7x * sin x = 1/2*[cos(7x - x) - cos(7x + x)] = 1/2*(cos 6x - cos 8x) sin 3x * sin 5x = 1/2*[cos(5x - 3x) - cos(5x + 3x)] = 1/2*(cos 2x - cos 8x) По уравнению cos 6x - cos 8x = cos 2x - cos 8x cos 6x = cos 2x По формуле тройного аргумента cos 3a = 4cos^3 a - 3cos a cos 6x = 4cos^3 2x - 3cos 2x = cos 2x 1) cos 2x = 0 2x = Pi/2 + Pi*k x = Pi/4 + Pi/2*k 2)4cos^2 2x - 3 = 1 cos^2 2x = 1 cos 2x = -1 2x = Pi + 2Pi*k x = Pi/2 + Pi*k 3) cos 2x = 1 2x = 2Pi*k x = Pi*k ответ: x1 = Pi/4 + Pi/2*k, x2 = Pi/2 + Pi*k, x3 = Pi*k
-4х-3х=-5-2
-7х=-7
х=1
у=-4+2=-2
у=3-5=-2
х=1 у=-2