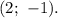![lim-x(x-9)( \sqrt[3]{(8-x)^2} + \sqrt[3]{64-x^2} + \sqrt[3]{(8+x)^2}/(8-x-8-x)=](/tpl/images/0442/3859/fe217.png)
![lim-x(x-9)( \sqrt[3]{(8-x)^2} + \sqrt[3]{64-x^2}+ \sqrt[3]{(8+x)^2} /(-2x) =](/tpl/images/0442/3859/484ff.png)
![lim(x-9)( \sqrt[3]{(8-x)^2} + \sqrt[3]{64-x^2} + \sqrt[3]{(8+x)^2}/2 =](/tpl/images/0442/3859/17840.png)
![(-9)( \sqrt[3]{64}+ \sqrt[]{64}+ \sqrt[3]{64})/2=(-9)(4+4+4)/2=(-9)*12/2=-9*6](/tpl/images/0442/3859/83997.png)
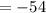
Объяснение:
Пусть точка 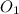 имеет координаты
имеет координаты 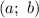 . Указаны также точки
. Указаны также точки 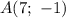 ,
, 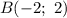 и
и 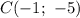 . Требуется же найти координаты точки
. Требуется же найти координаты точки 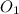 , притом таким образом, чтобы она была равноудалена от точек
, притом таким образом, чтобы она была равноудалена от точек 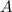 ,
,  и
и 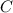 .
.
Расстояние от точки 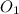 до точки
до точки 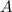 будет иметь такой вид:
будет иметь такой вид: 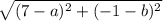 .
.
Расстояние от точки 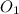 до точки
до точки  будет иметь такой вид:
будет иметь такой вид: 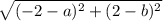 .
.
Расстояние от точки 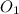 до точки
до точки 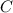 будет иметь такой вид:
будет иметь такой вид:
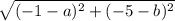 .
.
С этого момента допустимо оперировать квадратами расстояний вместо самих расстояний, так как от возведения обеих частей уравнений, которые мы получим позже, в квадрат получится полностью равносильное уравнение (ибо расстояние, очевидно, не может быть отрицательным).
Упростим все три выражения:
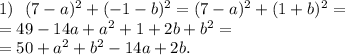
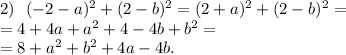
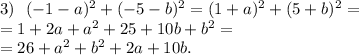
Условие же равноудалённости требует, чтобы эти три выражения были равны. Получается, что нужно решить такое уравнение:
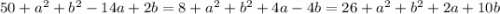 .
.
Уже здесь можно видеть, что к каждой части уравнения прибавлено выражение 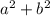 . Можно вычесть его из каждой части:
. Можно вычесть его из каждой части:
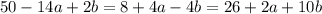 .
.
Применяя аксиому транзитивности отношения равенства (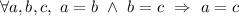 ), составим систему уравнений для нахождения
), составим систему уравнений для нахождения  и
и  :
:
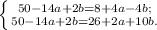
Упростим её:
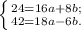
Поделим первое уравнение на 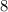 , а второе на
, а второе на 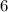 :
:
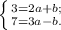
Решим систему методом сложения:
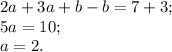
Отсюда находим  :
:
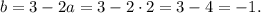
Обе координаты искомой точки найдены. ответом станет задаваемая ими точка: