Кусочно- заданная функция - это функция , которая на различных промежутках оси ОХ задаётся разными функциями. ( Как бы на разных "кусочках" оси ОХ задаются разные функции).
На промежутке (-∞ ; -2 ] функция представляет из себя гиперболу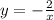 
. График гиперболы рисуем только на этом промежутке (сплошной линией), оставшаяся часть графика на промежутке (-2 ; +∞) стирается (либо рисуется пунктирной линией). Точка с абсциссой х= -2 , точка (-2,1) , принадлежит этому графику.
На промежутке (-2 ; 2] рисуем график у=|x|-1 . Это график функции у=|x|, который смещён на 1 единицу вниз по оси ОУ. Точка (-2,1) не принадлежит графику, а точка (2, 1) принадлежит графику.
На промежутке (2 ; + ∞) рисуем график функции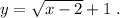 
Это график функции 
, смещённый вдоль оси ОХ на 2 единицы вправо и вдоль оси ОУ на 1 единицу вверх . Точка (2,1) не принадлежит графику функции.
График кусочно заданной функции нарисован сплошными линиями.
Сначала разберём таблицу. В первой строке - значения выборки, вторая строка - показывает сколько раз каждое значение встречается в выборке. Таким образом полная выборка будет такой: 2; 5; 5; 5; 7; 7; 8; 8; 8; 8. Количество значений в выборке будет равно 10 (это обозначается так n = 10).
1) Среднее арифметическое = (2 · 1 + 5 · 3 + 7 · 2 + 8 · 4) / 10 = 6,3
2) Дисперсия обозначается S² и вычисляется по формуле: сумму разностей квадратов значения выборки и её среднего арифметического поделить на (n-1). Получаем
S² = ( (2 - 6,3)² + (5 - 6,3)² + (5 - 6,3)² + (5 - 6,3)² + (7 - 6,3)² + (7 - 6,3)² + (8 - 6,3)² + (8 - 6,3)² + (8 - 6,3)² + (8 - 6,3)² ) / 10 - 1 = 4,01
3) Среднее квадратическое отклонение обозначается буквой ω:
ω = √S² = √4,01 = 2,002
4) Мода - это значение встречающееся в выборке чаще других, то есть
мода = 8
Если выборка содержит нечетное количество элементов, медиана равна (n+1)/2-му элементу.
Если выборка содержит четное количество элементов (как в нашем случае), медиана лежит между двумя средними элементами выборки и равна среднему арифметическому, вычисленному по этим двум элементам. То есть
медиана = (7 + 7) / 2 = 7
Если х = 0, то у = 45
Если у = 0, то (7,5х = -45) х = -6
ответ: (0; 45); (-6; 0).