Если с одной стороны находится произведение нескольких скобок, а с другой -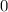 
, то мы имеем право применить метод интервалов.
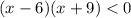
Для того, чтобы решить данное неравенство методом интервалов, сначала найдем те значения 
, которые при подсчете произведения дают .
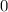То есть, это 
(уравнение 
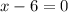) и 
(
).
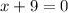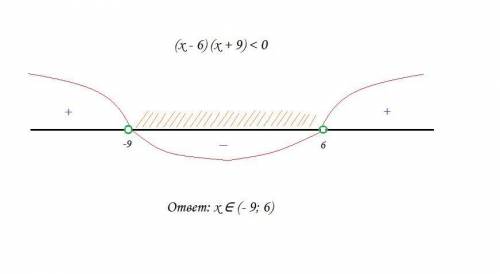
Ставим эти два числа на координатной прямой. Обозначаем их выколотыми точками, так как неравенство строгое. Смотрите рисунок в приложении.
Далее выставляем знаки на трех полученных промежутках. Можно, во-первых, выбрать какое-то число из промежутка и проследить за знаком произведения.
А можно обратить внимание на то, что перед нами - квадратичная функция, парабола, ветви которой направлены вверх. Поэтому на "боковых" промежутках произведение положительно (ставим "+"), а на "среднем" промежутке отрицательно (ставим "-").
Так как стоит знак "меньше", то мы берем промежуток посередине и ставим круглые скобки (как уже было оговорено, неравенство строгое). В общем, пишем ответ:
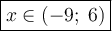
Если Вас интересует запись решения, то того, что происходит в приложенном файле, вполне достаточно.
2,5х + 15 = 2 * (х + 20)
2,5х + 15 = 2х + 40
2,5х - 2х = 40 - 15
0,5х = 25
х = 25 : 0,5
х = 50 (км/ч) - скорость автомобиля
2,5 * 50 = 125 (км) - расстояние между пунктами
ответ: 125 км.