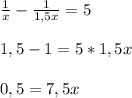
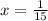 - скорость второго автомобиля
- скорость второго автомобиля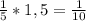 - скорость первого автомобиля
- скорость первого автомобиля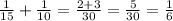 - скорость сближения автомобилей
- скорость сближения автомобилей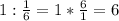 часов - через это время автомобили встретились
часов - через это время автомобили встретились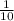 , то:
, то: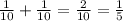 - была бы скорость сближения и встретились бы они через 5 часов, т.е.
- была бы скорость сближения и встретились бы они через 5 часов, т.е.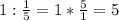 часов
часов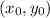 . В этом уравнении это сделать не совсем просто, поэтому воспользуемся теоремой:
. В этом уравнении это сделать не совсем просто, поэтому воспользуемся теоремой: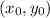 уравнения ах+ву=1.
уравнения ах+ву=1. 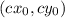 составляют решение
составляют решение 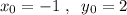 .
.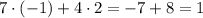
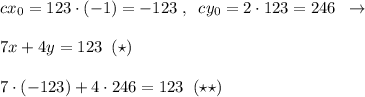
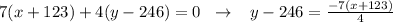
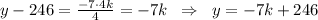
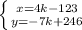 ,
, 
( sin²x-sinx·cosx)-(5cosx-5sinx)=0
sinx(sinx-cos)-5 (cosx-sinx)=0
sinx(sinx -cosx) - (-5) (sinx-cosx)=0
(sinx-cosx) (sinx+5)=0
1) sinx-cosx=0
разделим на cos x ( x≠π\2 +πn, n∈Z)
tgx-1=0
tgx=1
x=π\4+πn n∈Z
2) sinx+5=0
sinx=-5 нет решений