Скорее всего здесь речь идет об убывающей геометрической прогрессии...
для убывающей геометрической прогрессии Sn -> b1 / (1-q)
b1 / (1-q) = 3/4 ___ 4b1 = 3(1-q)
и сумма кубов тоже будет убывающей... => Sn3 -> (b1)^3 / (1-q^3)
(b1)^3 / (1-q^3) = 27/208
27(1-q)^3 / (64(1-q^3)) = 27/208
(1-q)^3 / ((1-q)(1+q+q^2)) = 4/13
(1-q)^2 / (1+q+q^2) = 4/13
13(1-2q+q^2) = 4(1+q+q^2)
13-26q+13q^2 - 4-4q-4q^2 = 0
3q^2 - 10q + 3 = 0
D = 100 - 4*9 = 64
q1 = (10 + 8)/6 = 3 ___ q2 = (10 - 8)/6 = 1/3
b1 = 1/2
Сумма квадратов членов прогрессии = (b1)^2 / (1-q^2) = 1/4 : 8/9 = 1/4 * 9/8 = 9/32
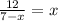
Для того чтобы решить дробно-рациональное уравнение нужно все перенести в левую часть, оставив в правой части лишь 0
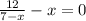
Приводим все к одному знаменателю. Для этого достаточно умножить х на знаменатель 7-х. Получается:
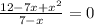
Когда дробь равна нулю? Когда числитель равен нулю, а знаменатель не равен нулю. Значит пишем:
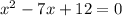 ,
, 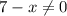
Решаем квадратное уравнение и обычное неравенство. Получаем значения:
x=3, х=4 и 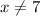
В ответ пишем только ответы числителя, если они не совпадают с ответами знаменателя. Если совпадают, то их нельзя писать, т.к. при этих значениях дробь не имеет смысла, потому что на ноль делить нельзя. Т.е. если бы у нас в квадратном уравнении получился еще ответ х=7, то мы бы его в ответ не записывали по указанным ранее причинам. Но в нашем случае никаких совпадений нет, поэтому пишем:
ответ: х=3 и х=4