Пусть х (км/ч) - скорость течения, тогда (10+х) - скорость моторной лодки по течению, а (10-х) - скорость моторной лодки против течения. Составим уравнение.
39:(10+х)+28:(10-х)=7
39(10-х)+28(10+х)=7(10+х)(10-х)
390-39х+280+28х=7(100+10х-10х-х^2)
670-11х=700-х^2
7x^2-11х+670-700=0
7х^2-11х-30=0 -квадратное уравнение
Решаем квадратное уравнение.
D (Дискриминант уравнения) = b 2 - 4ac = 961
х1=(-b+√D)/2a=(11+31)/(2*7)=42/14=3
х2=(-b-√D)/2a=(11-31)/(2*7)=-20/14=-10/7
Скорость течения: 3 км/ч
Проверка:
39:(10+3)+28:(10-3)=7
39:13+28:7=7
3+4=7
7=7
ответ: скорость течения реки 3 км/ч
1) 3 sin²x +9sinx=0
Вынесем за скобку общий множитель:
3sinx(sinx+3)=0
Произведение равно 0, когда хотя бы один из множителей равен 0.
3sinx=0(по частным формулам) sinx+3=0
sinx=-3 (такого быть не может, т.к. синус принимает значения от -1, до : [-1;1])
ответ: 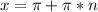
2) sin²x-2sinx-3=0
Это квадратное уравнение, обозначим sinx=a, a принимает значения [-1;1]
a²-2a-3=0
Корни находим по теореме Виета
a1=3 a2=-1
sinx=-1 ( по частным формулам)
3) cos²x-3sinx-3=0
По основной формуле заменим косинус( cos²x=1-sin²x) и получим квадратное уравнение:
1-sin²x-3sinx-3=0
sin²x+3sinx+2=0
sinx=a, a принимает значения [-1;1-]
a²+3a+2=0
a1=-2 a2=-1
sinx=-1
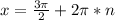
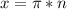
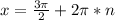
D(y): x=3(равно зачёркивай) или (- знак бесконечности; 3) v (3;+знак бесконечности)