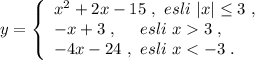
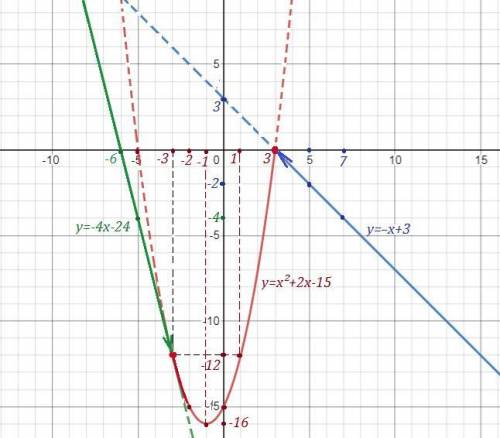
Кусочная функция на графике нарисована сплошными линиями .
Рисуем параболу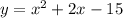 
при изменении переменной "х" в пределах от -3 до 3 , 
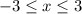. Ветви параболы направлены вверх, вершина параболы в точке (-1;-16) . Точки (3;0) и (-3;-12) принадлежат графику .
Прямую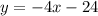 
рисуем при 
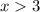. Точка (3;0) не принадлежит графику .
Прямую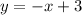 
рисуем при 
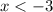. Точка (-3;-12) не принадле-жит графику .
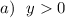при 
.
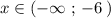б) область значений функции: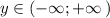 
,
при х=5 значение функции у=-2 ,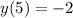 
.
в) пересечение с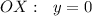 
при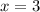 
, 
.
пересечение с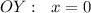 
, если 
.
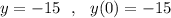г) y(x) возрастает при ![x\in [-1\ ;\ 3\ ]](/tpl/images/1787/8534/dc20e.png)
.
y(x) убывает при ![x\in (-\infty ;-1\ ]\cup [\ 3\ ;+\infty \, )](/tpl/images/1787/8534/485e8.png)
,
В решении.
Объяснение:
Катер 36 км против течения и 54 км по течению, затратив на весь путь 6 часов. Найдите собственную скорость катера, если скорость течения равна 3 км/час.
Формула движения: S=v*t
S - расстояние v - скорость t – время
х - собственная скорость катера.
х + 3 - скорость катера по течению.
х - 3 - скорость катера против течения.
54/(х + 3) - время катера по течению.
36/(х - 3) - время катера против течения.
По условию задачи уравнение:
54/(х + 3) + 36/(х - 3) = 6
Умножить все части уравнения на (х - 3)(х + 3),чтобы избавиться от дробного выражения:
54*(х - 3) + 36*(х + 3) = 6(х² - 9)
54х - 162 + 36х + 108 = 6х² - 54
Привести подобные члены:
-6х² + 90х = 0/-1
6х² - 90х = 0 неполное квадратное уравнение
6х(х - 15) = 0
6х = 0
х₁ = 0, отбрасываем, как не соответствующее условию задачи.
х - 15 = 0
х₂ = 15 (км/час) - собственная скорость катера.
Проверка:
54/18 + 36/12 = 3 + 3 = 6 (часов), верно.
2) 65+61=126 (д) изготавливает ученик за 5 часов
3) 126:5=25 (ост 1) (д) изготавливает ученик
ответ : 1 час роботы ученик изготавливает 25 деталей а мастер за 1 час изготавливает 13 деталей