ответобьяснение
Объяснение:
при имеющемся знаменателе необходимо производить деление такого типа функции как
y
=
x
+
2
⋅
x
x
4
−
1
;
при наличии переменной под знаком корня необходимо обращать внимание на корень четной степени типа
y
=
√
x
+
1
или
y
=
x
√
2
3
⋅
x
+
3
;
при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как
y
=
5
⋅
(
x
+
1
)
−
3
,
y
=
−
1
+
x
1
1
3
,
y
=
(
x
3
−
x
+
1
)
√
2
, которые определены не для всех чисел;
при наличии переменной под знаком логарифма или в основании вида
y
=
ln
x
2
+
x
4
или
y
=
1
+
log
x
−
1
(
x
+
1
)
причем основание является числом положительным, как и число под знаком логарифма;
при наличии переменной, находящейся под знаком тангенса и котангенса вида
y
=
x
3
+
t
g
(
2
⋅
x
+
5
)
или
y
=
c
t
g
(
3
⋅
x
3
−
1
)
, так как они существуют не для любого числа;
при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида
y
=
a
r
c
sin
(
x
+
2
)
+
2
⋅
x
2
,
y
=
a
r
c
cos
(
|
x
−
1
|
+
x
)
, область определения которых определяется ни интервале от
−
1
до
1
.при имеющемся знаменателе необходимо производить деление такого типа функции как
y
=
x
+
2
⋅
x
x
4
−
1
;
при наличии переменной под знаком корня необходимо обращать внимание на корень четной степени типа
y
=
√
x
+
1
или
y
=
x
√
2
3
⋅
x
+
3
;
при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как
y
=
5
⋅
(
x
+
1
)
−
3
,
y
=
−
1
+
x
1
1
3
,
y
=
(
x
3
−
x
+
1
)
√
2
, которые определены не для всех чисел;
при наличии переменной под знаком логарифма или в основании вида
y
=
ln
x
2
+
x
4
или
y
=
1
+
log
x
−
1
(
x
+
1
)
причем основание является числом положительным, как и число под знаком логарифма;
при наличии переменной, находящейся под знаком тангенса и котангенса вида
y
=
x
3
+
t
g
(
2
⋅
x
+
5
)
или
y
=
c
t
g
(
3
⋅
x
3
−
1
)
, так как они существуют не для любого числа;
при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида
y
=
a
r
c
sin
(
x
+
2
)
+
2
⋅
x
2
,
y
=
a
r
c
cos
(
|
x
−
1
|
+
x
)
, область определения которых определяется ни интервале от
−
1
до
1
.
А) 480
Б)1.6
Объяснение:
А) так как размер плит уменьшился в два раза, то количество плит увеличится в два раза. Следовательно 240*2=480
так как размер плит уменьшился в два раза, то количество плит увеличится в два раза. Следовательно 240*2=480Б) Вычисляем сколько кг металла нужно для изготовления одной детали
так как размер плит уменьшился в два раза, то количество плит увеличится в два раза. Следовательно 240*2=480Б) Вычисляем сколько кг металла нужно для изготовления одной детали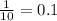 
так как размер плит уменьшился в два раза, то количество плит увеличится в два раза. Следовательно 240*2=480Б) Вычисляем сколько кг металла нужно для изготовления одной детали 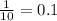для изготовления 1 детали требуется 0.1 кг металла.
так как размер плит уменьшился в два раза, то количество плит увеличится в два раза. Следовательно 240*2=480Б) Вычисляем сколько кг металла нужно для изготовления одной детали 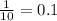для изготовления 1 детали требуется 0.1 кг металла.Далее находим сколько кг металла нужно для изготовления 16 деталей
так как размер плит уменьшился в два раза, то количество плит увеличится в два раза. Следовательно 240*2=480Б) Вычисляем сколько кг металла нужно для изготовления одной детали 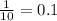для изготовления 1 детали требуется 0.1 кг металла.Далее находим сколько кг металла нужно для изготовления 16 деталей0.1*16= 1.6кг металла
V= Sоснования *H= abc
Ширину обозначим b.
Полная пов-сть :
Sполная=2*а*b +2hа +2hb =2b(а+h) + 2hа. Отсюда:
2b(а+h)=S - 2hа
b=(S-2hа):2(а+ h)
Найти отсюда b, подставив свои значения S а также а и h.
Затем площадь основания аb умножить на высоту. Получится
V=(S-2hа):{2(а+ h)} *а*h объем параллелепипеда.