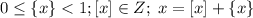На трёх полках расположены книги так, что на второй полке книг вдвое больше чем на первой, а на третьей - вдвое больше, чем на второй. определите, сколько книг на каждой полке, если всего на трех полках 154 книги. решается уравнением, вам,

👇

Увидеть ответ

Ответ:

070974zZ

01.06.2022

2x+4x+x=154 7x=154 x=154:7 x=22 на первой полке 22*2=44 на второй 22*44=88 на третьей я всё проверил всё правильно

4,8(33 оценок)

Открыть все ответы

Ответ:

Тунеков23

01.06.2022

1. Үнді өзенінің жоғарғы ағысына бес өзен келіп қосылады. Бұл аймақ қалай аталады?

2. Үндістанға солтүстіктен келген көшпелі тайпаларды ата?

3. Үнді қыздарының ұлттық киімі қалай аталады?

4. Б. з. б ҮІ ғасырларда Ганга өзенінің төменгі ағысы бойында пайда болған мемлекет?

5. Үндістанның Агра қаласында орналасқан тарихи ескерткішті атаңыз?

6. Үндістанның солтүстігінен басталып, оңтүстік шығысқа қарай ағатын өзен?

7. Өз дәрежесі бойынша өмір сүруге тиісті тұйық топ?

8. Үнділерде тайпа көсемдері қалай аталған?

9. Маурия әулетінің негізін қалаған кім?

10. Брахма құдайдың аяғынан жаралған төртінші топ өкілдері?

4,7(83 оценок)

Ответ:

hjhytu

01.06.2022

По определению, 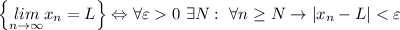$\left\{\underset{n\rightarrow\infty}{lim}x_n=L\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n-L\right|$

Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение 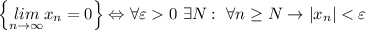$\left\{\underset{n\rightarrow\infty}{lim}x_n=0\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n\right|$

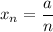
2) $x_n=\dfrac{a}{n}$

|x_n|

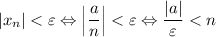
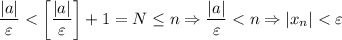
А значит, если взять $N=\left[\dfrac{|a|}{\varepsilon}\right] +1$ (*), $\forall\;n\geq N\to |x_n|$ . И правда: $\dfrac{|a|}{\varepsilon}$

(*) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{|a|}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)

А это и означает, что предел данной последовательности равен 0

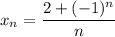
4) $x_n=\dfrac{2+(-1)^n}{n}$

|x_n|

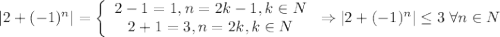
$|2+(-1)^n|=\left\{\begin{array}{c}2-1=1,n=2k-1,k\in N \\2+1=3,n=2k,k\in N \end{array}\right. \Rightarrow |2+(-1)^n|\leq 3\; \forall n\in N$

А значит, если взять $N=\left[\dfrac{3}{\varepsilon}\right] +1$ (**), $\forall\;n\geq N\to |x_n|$ . И правда: $\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|$

(**) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{3}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)

А это и означает, что предел данной последовательности равен 0

___________________________

2) a=1. Тогда 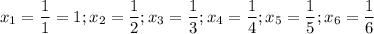$x_1=\dfrac{1}{1}=1; x_2=\dfrac{1}{2}; x_3=\dfrac{1}{3}; x_4=\dfrac{1}{4}; x_5=\dfrac{1}{5}; x_6=\dfrac{1}{6}$

$x_1=\dfrac{2+(-1)^1}{1}=1;\;x_2=\dfrac{2+(-1)^2}{2}=1\dfrac{1}{2};\;x_3=\dfrac{2+(-1)^3}{3}=\dfrac{1}{3};\;x_4=\dfrac{2+(-1)^4}{4}=\dfrac{3}{4};\;x_5=\dfrac{2+(-1)^5}{5}=\dfrac{1}{5};\;x_6=\dfrac{2+(-1)^6}{6}=\dfrac{1}{2}.$