Question

1.вычислить: 1) 2,8: 14/15 2) 1,8·2 2/3 3) (3 1/3)² · 0,6 4) (-0,8)²÷0,4 2.выполнить деление с точностью до 0,01: 1) 25: 9 2) 335: 3 3) 7,3: 0,7 4) 0,5: 0,06 3.решить уравнение: 1) √x=0; 2) √x=1 3)√x=100 4) √x=25

Answer 1

   1.

1) $\displaystyle 2,\! 8:\frac{14}{15} =\frac{28}{10} \cdot \frac{15}{14} =\frac{2\cdot 2\cdot 7\cdot 5\cdot 3}{2\cdot 5\cdot 2\cdot 7} =\frac31 =\bold{3}$

2) $\displaystyle 1,\! 8\cdot 2\frac23 =\frac{18}{10} \cdot \frac{2\cdot 3+2}3 =\frac95 \cdot \frac83 =\frac{3\cdot 3\cdot 8}{5\cdot 3}=$

$\displaystyle =\frac{24}{5} ^{(2}=\frac{48}{10} =\bold{4,\! 8}$

3) $\displaystyle \bigg( 3\frac13 \bigg) ^2\cdot 0,\! 6=\bigg( \frac{10}3 \bigg) ^2\cdot \frac6{10} =\frac{100}9 \cdot \frac6{10} =$

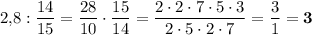
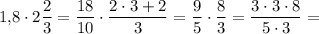
$\displaystyle \frac{10\cdot 10\cdot 3\cdot 2}{3\cdot 3\cdot 10} =\frac{20}3 =\frac{18+2}3 =\bold{6\frac23 }$

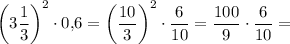
4) (-0,8)² : 0,4 = 0,64:0,4 = (0,04·16):0,4 = 0,1·16 = 1,6

   2.

Вычислим 3 знака после запятой и округлим до двух.

ответ на это задание смотри в приложении.

   3.

1) √x = 0;  x = 0² = 0

ответ: x = 0.

2) √x = 1;  x = 1² = 1 > 0

ответ: x = 1.

3) √x = 100;  x = 100² = 10 000 > 0

ответ: x = 10 000.

4) √x = 25;  x = 25² = 625 > 0

ответ: x = 625.