41-32х≥0;
9-3х≥0
5+х≥0
ОДЗ: х ∈[-5; 41/32]
Перепишем уравнение в виде
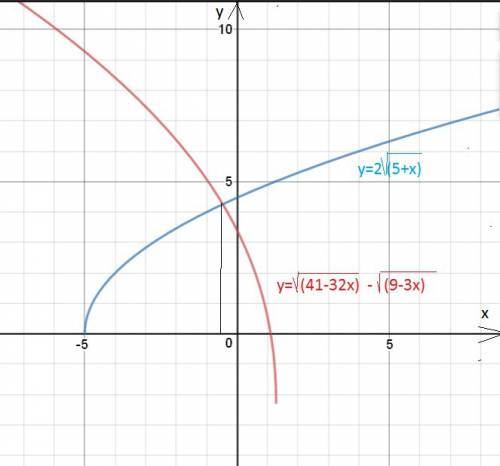
√(41-32x)=2√(5+x)+√(9-3x)
Возводим в квадрат.
41-32х=4(5+х)+4√(5+х)·√(9-3х)+9-3х
4√(5+х)·√(9-3х)=12-33х
Возводим в квадрат при условии 12-33х≥0 ⇒ х ≤12/33.
16(5+х)(9-3х)=144-792х+1089х²;
1137х²-696х-576=0
379х²-232х-192=0
D=(-232)²-4·379·(-192)=53 824+291 072=344 896
x=(232-√344896)/758≈-0,47 или х=(232+√344896)/758≈1,08 - не удовлетворяет условию х ≤12/33, поэтому не является корнем уравнения
task/29646731 Чему равно наибольшее значение функции y=x²-3x+2 на отрезке [-5;5] ?
y= x²-3x+2 ⇔ y = (x - 3/2)² - 1/4 ⇒ min y = - 1/4 , при x = 3 /2 ∈ [-5;5]
График парабола ; A(0;2) ; B(1 ;0) ; C(2 ; 0) ; G(1,5 ; -0;25) точки графика
Функция убывает , если x ∈ [-5 ; 3/2] , возрастает , если x ∈ [ 3/2 ; 5] .
y( -5) =(-5)² - 3*(-5) +2 = 42. y( 5) =5² - 3*5 +2 = 12 .
ответ: 42.
ИЛИ
* Непрерывная на отрезке функция достигает максимума и минимума * *
y ' = (x²-3x+2) ' = (x²) '- (3x) '+(2) ' =2x -3*(x)' +0 =2x -3 . y' =0 ⇒ x =3/2
y ' " - " " +"
1,5 (критическая точка x=1,5 →точка минимума)
y ↓ min ↑
y( -5) =(-5)²- 3*(-5) +2 = 42. y (1,5)=1,5²-3*1,5 +2= -0,25 ; y( 5) =5²- 3*5 +2 = 12 .
у min = y(1,5) = - 0,25 ; у max = y(-5) = 42.
(a-3)x^2+11x+a^2-9=0 является неполным квадратным?
(a-3)x^2+11x+(a-3)(a+3)=0
при a=3 оно перестает быть квадратным
при a=-3 -6x^2+11x=0