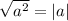, к нашему выражению применимо вот так: 
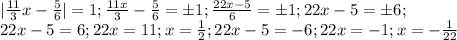. ответ: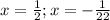 
Решение: Первые три уравнения простейшие тригонометрические уравнения
sin x=1
x=pi\2+2*pi*k, k- любое целое
cos x=1
x=2*pi*k, k – любое целое
tg x=1
x=pi\4+pi*k, k – любое целое
sin^2 x-cos^2 x=0
Если cos x=0, sin^2=1, и 1-0=1, а значит не равно 0. При делении на cos^2 x, потери корней не будет, делим, получим уравнение
tg^2 x=1
x=pi\4+pi*k, где k – любое целое
x=-pi\4+pi*n, где n – любое целое
объединяя решения, окончательно получим x=pi\4+pi\2*k, k – любое целое
произведение при умножении любого числа на 5 заканчивается либо на 5 либо на 0, 0 впереди числа стоять не может, следовательно должна стоять цифра 5. Возьмем для примера двузначное число 59 (после 5 должна стоять наибольшая цифра, чтобы получить максимальное число), при перестановке 5 на конец числа получаем число 95, что больше предыдущего более, чем в два раза, для того,чтобы получить число больше предыдущего в 5 раз, оно должно как минимум начинаться с двух (и менее), но мы ужевыяснили что число должноначинаться с 5, поэтомы такого числа нет
