Question

Спри каких значениях а =0 значение дроби a)(а^3-9a )/a^2+a-12 б)(a^5+2a^4 )/a^3+a+10 в)( a^5-4a^4+4a^3)/a^4-16 надо с решениями

Answer 1

a) $\frac{a^{3}-9a}{a^{2}+a-12}=0$

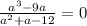
Область допустимых значений

$a^{2}+a-12\neq0$ (т. к. на нуль делить нельзя)

рассмотрим числитель

$a^{3}-9a=0$

$a(a^{2}-9)=0$

$a_{1}=0$

$a^{2}-9=0$

$a^{2}=9$

$a=\sqrt{9}$$a=\sqrt{9}$$a=\sqrt{9}$

$a_{2}=3$

$a_{3}=-3$

рассмотрим знаменатель

$a^{2}+a-12\neq0$

Cчитаем дискриминант:

$D=1^{2}-4\cdot1\cdot(-12)=1+48=49$

Дискриминант положительный

$\sqrt{D}=7$

Уравнение имеет два различных корня:

$a_{1}=\frac{-1+7}{2\cdot1}=\frac{6}{2}=3$

$a_{2}=\frac{-1-7}{2\cdot1}=\frac{-8}{2}=-4$

следовательно $a\neq3$ и $a\neq-4$$a\neq-4$

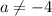
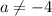
ответ: при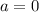 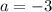$a=0$; $a=-3$ данное выражение равно нулю.

б)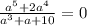 $\frac{a^{5}+2a^{4}}{a^{3}+a+10}=0$

Область допустимых значений

$a^{3}+a+10\neq0$ (т. к. на нуль делить нельзя)

рассмотрим числитель

$a^{5}+2a^{4}=0$

$a^{4}(a+2)=0$

$a_{1}=0$

$a+2=0$

$a_{2}=-2$

рассмотрим знаменатель

$a^{3}+a+10\neq0$

корнем этого уравнения является, что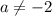 $a\neq-2$

ответ: при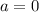 $a=0$ данное выражение равно нулю.

в)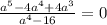 $\frac{a^{5}-4a^{4}+4a^{3}}{a^{4}-16}=0$

Область допустимых значений

$a^{4}-16\neq0$ (т. к. на нуль делить нельзя)

рассмотрим числитель

$a^{5}-4a^{4}+4a^{3}=0$

$a^{3}(a^{2}-4a+4)=0$

$a_{1}=0$

$a^{2}-4a+4=0$

Заметим, что данное выражение можно свернуть в квадрат 

$(a-2)^{2}=0$

Cледовательно уравнение имеет один корень:

$a_{2}=2$

рассмотрим знаменатель

$a^{4}-16\neq0$

$a^{4}\neq16$

$\sqrt[4]{a}=16$

$a_{1}\neq2$

ответ: при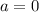 $a=0$ данное выражение равно нулю.