Пусть х км/ч - скорость одного поезда, тогда (х + 10) км/ч - скорость другого поезда. Уравнение:
400/х - 400/(х+10) = 2
400 · (х + 10) - 400 · х = 2 · х · (х + 10)
400х + 4000 - 400х = 2х² + 20х
2х² + 20х - 4000 = 0
Разделим обе части уравнения на 20
0,1х² + х - 200 = 0
D = b² - 4ac = 1² - 4 · 0,1 · (-200) = 1 + 80 = 81
√D = √ 81 = 9
х₁ = (-1-9)/(2·0,1) = (-10)/(0,2) = -50 (не подходит, т.к. < 0)
х₂ = (-1+9)/(2·0,1) = 8/(0,2) = 40 км/ч - скорость одного поезда
40 + 10 = 50 км/ч - скорость другого поезда
ответ: 40 км/ч и 50 км/ч.
Проверка:
400/40 - 400/50 = 10 - 8 = 2 (ч) - разница
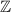разделим на три класса:
, где + обозначает операцию объединения и изначает, что множества 
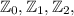дисъюнктны.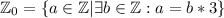
.
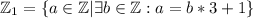
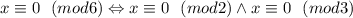
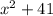делится на два (сумма нечетных чисел четна), то есть выражение все равно делится на два, первое условие выполнено. Докажем, что x делится на 3:
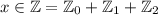, то рассмотрим три случая:
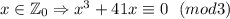так как 
.
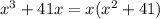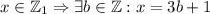
для каких-то 
, то есть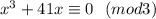 
.
.
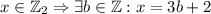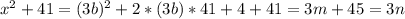для каких-то , то есть .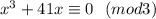
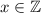выражение 
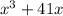делится на 6.
520разделить на 65 =8часов