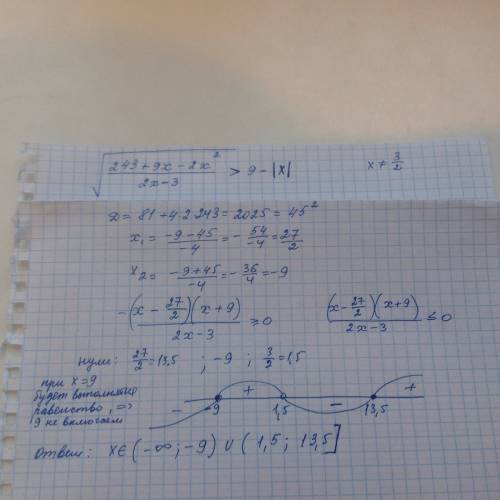
Для решения этой задачи используем формулы арифметической прогрессии.
а₁=5 [в первый день 5 капель]
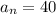[день, в который нужно выпить 40 капель]
d=5 [разность арифметической прогрессии, т.к. каждый день дозировка увеличивается на одну и ту же величину - 5 капель]
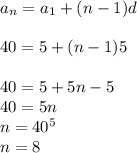
На восьмой день дозировка составит 40 капель.
По формуле суммы n первых членов арифметической прогрессии найдм сколько всего капель нужно выпить больному за 8 дней.
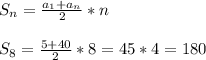
180 капель должен выпить больной за первые 8 дней лечения.
В последний период лечения больной должен уменьшать дозировку каждый день на 5 капель, и с дозировки в 40 капель дойти до 5 капель.
На это ему понадобиться 8 дней (также, как и в первый период лечения).
Суммарное количество капель, которые должен выпить больной за эти 8 дней, составит 180.
В середине лечения больной должен три дня подряд пить по 40 капель. Два раза по 40 капель мы уже учли. Поэтому к общей сумме добавим только 40.
180+180+40 = 400 (капель) - должен выпить больной за весь период лечения.
В одном пузырьке содержится 200 капель лекарства. Значит больному нужно купить 400:200 = 2 пузырька лекарства.
ответ: 2 пузырька.
ответ: 286,5 см².
Объяснение:
Дано. ABCD - прямоугольная трапеция.
BD - диагональ является биссектриса острого угла.
найдите площадь трапеции, если боковые стороны равны 10 см и 20 см.
Решение.
Биссектриса в трапеции отсекает равнобедренный треугольник.
ВС=CD=20 см.
Проведем высоту СЕ. Из треугольника CED:
DE=√20²-10²=√400-100=√300 = 10√3 =17,3 см. Тогда
основание AD=AE+ED=20+17,3 = 37,3 см.
Площадь трапеции S=h(a+b)/2 = 10(20+37,3)/2=10*57,3/2=286,5 см².
Площадь трапеции равна 286,5 см².
