ответ: 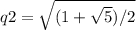
Объяснение:
Пусть самый короткий катет равен b1- первый член геометрической прогрессии, а его квадрат b1².
Тогда второй член геометрической прогрессии - больший катет равен b1·q ( q -знаменатель прогрессии). Тогда его квадрат равен
b1²·q². Тогда 3-ий член геометрической прогрессии - гипотенуза равен b1·q² , а его квадрат равен 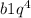
Тогда по теореме Пифагора
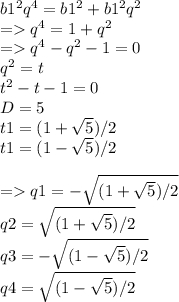
q3 и q4 не годятся , так как число под корнем не может быть меньше 0.
q1 не годится, так как знаменатель не может быть В ДАННОМ СЛУЧАЕ меньше 0 , иначе второй катет будет меньше 0, что быть не может.
Остается только q2
х=0
2)х(х+25)=0
х1=0
х2=25
3)(х-6)(х+6)=0
х1=6 х2=-6
4)х1+х2=-5
то х1=1 х2=-6
5)D=25-16=9 √D=3
x1=2/8=1/4
x2=8/8=1
5x²-2x=6x-3
5x²-8x+3=0
D=64-60=4 √D=2
x1=1 x2=0.6