Дробь 
является неправильной рациональной дробью, так как степени многочленов в числителе и в знаменателе одинаковые и равны 1. Значит можно выделить целую и дробную часть неправильной дроби. Так как в знаменателе стоит многочлен 1 степени (линейная ф-ция) х+1, то и в числителе выделим х+1. Для этого надо вынести за скобки коэффициент (-5), который стоит перед х, и записать в скобках (х+1). Так как -5(х+1)=-5х-5, то , чтобы выражение не изменилось, надо добавить (+5), получим:
.
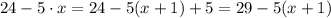Если в дальнейшем надо записать целую и дробную части неправильной рац. дроби, то
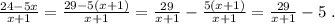
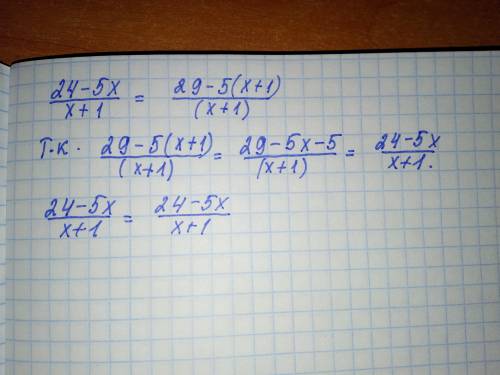
Рассмотрим указанный диапазон натуральных чисел как расширенный натуральный ряд (то есть такой, куда входит 0). Разобьём этот ряд на пары. Получим:
0;999999999
1;999999998
2;999999997
3;999999996
...и так далее.
Одно число (1000000000) останется без пары.
Из составленного понятно, что сумма цифр в одной паре равна: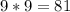 
.
Так как мы разбили ряд на две равные части, количество пар будет равно:
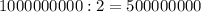
Зная это, умножим сумму цифр в одной паре на количество пар и добавим 1, так как одно число у нас осталось без пары.
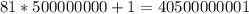
ответ: 40500000001
{x-5<25⇒x<30
x∈(5;30)
2)x-7>0⇒x>7
2x+1>0⇒x>-1/2
x∈(7;∞)
log(2)(2x+1)-log(2)(x-7)²=3
log(2)[(2x+1)/(x-7)²=3
(2x+1)/(x-7)²=8
2x+1=8x²-112x+392
8x²-114x+391=0
D=12996-12512=484
x1=(114-22)/16=5,75
x2=(114+22)/16=8,5