Question

Представьте выражение в виде произведения двух многочленов: 1)2a*(m+n)+b*(m+n) 2)8*(x-1)+(x-1)^2 3)3c*(x-y)-2d*(x-y) 4)3ab*(x+2y)+c^2*(x+2y) 5)9a^2*(x-2y)-b^2*(x-2y)+(x-2y)^2 6)3a*(2x-7)+5b*(2x--7)^2 разложите на множители: 1)5x*(2a-3b)+2y*(2a-3b)+z*(2a-3b) 2)7*(c+2)+(c+2)^2-b*(c+2) 3)2ab^2*(3x+y)+4a*(3x+y_ 4)2ab^2*(x^2-x+1)-15x^2*y*(x^2-x+1)

Answer 1

1)2a*(m+n)+b*(m+n)=(m+n)(2a+b)
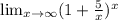
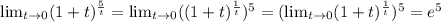
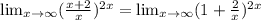
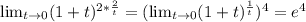
2)8*(x-1)+(x-1)²=(x-1)(8+x-1)=(x-1)(7+x)
3)3c*(x-y)-2d*(x-y)=(x-y)(3c-2d))
4)3ab*(x+2y)+c²*(x+2y)=(x+2y)(3ab+c²)
5)9a²*(x-2y)-b²*(x-2y)+(x-2y)²=(x-2y)(9a²-b²+x-2y)
6)3a*(2x-7)+5b*(2x-7)-(2x-7)²=(2x-7)(3a+5b-2x+7)

Разложите на множители:
1)5x*(2a-3b)+2y*(2a-3b)+z*(2a-3b)=(2a-3b)(5x+2y+z)
2)7*(c+2)+(c+2)²-b*(c+2)=(c+2)(7+c+2-b)=(c+2)(9+c-b)
3)2ab²*(3x+y)+4a*(3x+y)=2a(3x+y)(b²+2)
4)2ab²*(x²-x+1)-15x²*y*(x²-x+1) = (x²-x+1)(2ab²-15x²y)