Объяснение:
Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k=tg α.
Угол наклона прямой равняется 0 только при параллельности ох и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0. Значит, вид уравнения будет y=b.
Если угол наклона прямой y=kx+b острый, тогда выполняются условия 0<α<
π
2
или 0°<α<90°. Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию tg α>0, причем имеется возрастание графика.
Если α=
π
2
, тогда расположение прямой перпендикулярно ох. Равенство задается при равенства x=c со значением с, являющимся действительным числом.
Если угол наклона прямой y=kx+b тупой, то соответствует условиям
π
2
<α<π или 90°<α<180°, значение углового коэффициента k принимает отрицательное значение, а график убывае
Xn= 8 n-4
Xn= 4*3
Объяснение:
Последовательности можно задавать различными среди которых особенно важны три: аналитический, словесный и рекуррентный. В этой задаче рассмотрим два задания последовательности:
рекуррентное задание последовательности:
это такой задания последовательности, при котором указывают правило, позволяющее вычислить n-й член последовательности, если известны её предыдущие члены.
Аналитическое задание последовательности:
говорят, что последовательность задана аналитически, если указана формула её n-го члена yn=f(n).
1. Рассмотрим заданную рекуррентным последовательность x1=4,xn=xn−1+8, n=2,3,4...
n-й член последовательности получается из предыдущего (n−1)-го члена прибавлением к нему числа 8.
Тем самым получаем последовательность:
4; 12; 20; 28...
Для того чтобы последовательность можно было задать аналитически, преобразуем выражение:
xn=4+8(n−1)=8n−4.
Итак, мы получили формулу n-го члена заданной последовательности:
xn=8n−4.
2. Рассмотрим вторую, заданную рекуррентным последовательность x1=4,xn=3xn−1, n=2,3,4...
n-й член последовательности получается из предыдущего (n−1)-го члена умножением его на 3.
Тем самым получаем последовательность:
4; 12; 36; 108...
И формула n-го члена заданной последовательности:
xn=4⋅3n−1.
Если правильно понимаю, здесь подойдет последовательность Фибоначчи. Первые два члена равны 1. Остальные члены вычисляются как сумма двух предыдущих. То есть 1, 1, 2, 3, 5, 8, 13, 21, ... Рекуррентной формулой для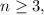
где n - из натурального ряда будет 