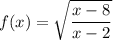
Подкоренное выражение должно быть неотрицательным, а знаменатель не равен нулю. При записи первого условия, второе учитывается. Тогда имеем:
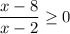
Решим методом интервалов:
Отмечаем на координатной прямой точки, в которых выражения из знаменателя и числителя обращаются в ноль. И выкалываем 2 т.к. на ноль делить нельзя. Мы получили 3 интервала. Перед дробью знак положителен, поэтому на правом интервале ставим "плюс", далее чередуем знак через каждую отмеченную точку (нету чётных степеней, где знак может не измениться). Нас интересует, когда больше или равно, поэтому выбираем интервалы с плюсом, учитывая их границы.
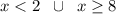
ответ: x∈(-∞;2)∪[8;+∞).

А) 2+0=2 и 4-0=4 верно, значит является
Б) 0+2=2 и -2=4 второе не верно, значит не является
2) умножим второе уравнение на 3, получим
3х-3у=12, теперь уравнения складываем
6х=15
Х=15/6=5/2=2,5
У=4-Х=4-2,5=1,5
3) из первого уравнения у=Х-4
5у/10=2х/10
5у=2х
5х-20-2х=0
3х=20
Х=20/3
Х=6целых и 2/3
У=2 целых и 2/3
4) если разность равна 0, значит они одинаковы, а если сумма 8, то значит каждое из чисел равно 4
ответ: двузначное число=44