В решении.
Объяснение:
14.3.
1) а₁ = 3; d = 3; an = 27; n = ? Sn = ?
Формула:
an = a₁ + d(n - 1) ⇒ n = (an - a₁)/d + 1
n = (27 - 3)/3 + 1 = 9;
n = 9.
Формула:
Sn = ((2a₁ + d(n - 1))/2 * n
S₉ = (2*3 + 3*8)/2 * 9 = 135;
S₉ = 135.
2) а₁ = 14; d = 6; an = 84;
Формула:
an = a₁ + d(n - 1) ⇒ n = (an - a₁)/d + 1
n = (84 - 14)/6 + 1 = 12 и 2/3;
Число n не может быть дробным. Опечатка?
Если d = 7. то:
n = (84 - 14)/7 + 1 = 11;
n = 11.
Формула:
Sn = ((2a₁ + d(n - 1))/2 * n
S₁₁ = (2*14 + 6*10)/2 * 11 = 484;
S₁₁ = 484.
3) а₁ = -5,4; d = 1,8; an = 30,6;
Формула:
an = a₁ + d(n - 1) ⇒ n = (an - a₁)/d + 1
n = (30,6 + 5,4)/1,8 + 1 = 21;
n = 21.
Формула:
Sn = ((2a₁ + d(n - 1))/2 * n
S₂₁ = (2*(-5,4) + 1,8*20)/2 * 21 = 264,6;
S₂₁ = 264,6.
4) а₁ = -7,3; d = -2,6; an = -30,7;
Формула:
an = a₁ + d(n - 1) ⇒ n = (an - a₁)/d + 1
n = (-30,7 + 7,3)/(-2,6) + 1 = 10;
n = 10.
Формула:
Sn = ((2a₁ + d(n - 1))/2 * n
S₁₀ = (2*(-7,3) - 2,6*9)/2 * 10 = -190;
S₁₀ = -190.
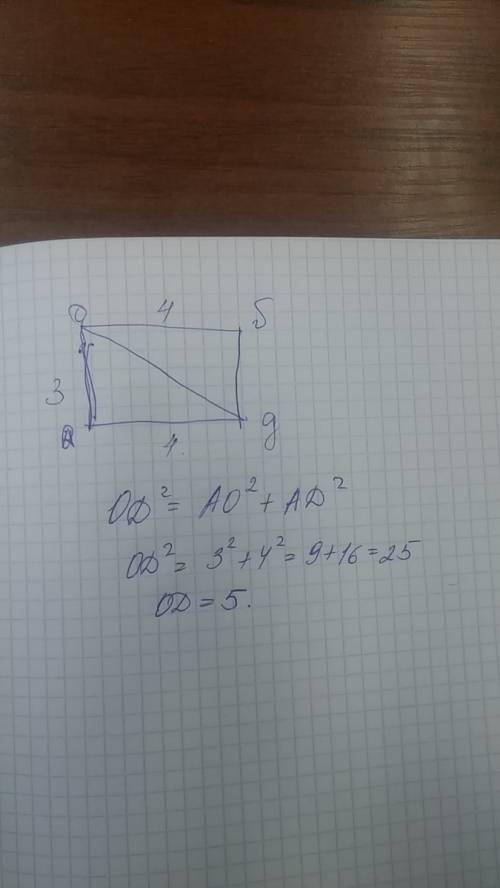
В решении.
Объяснение:
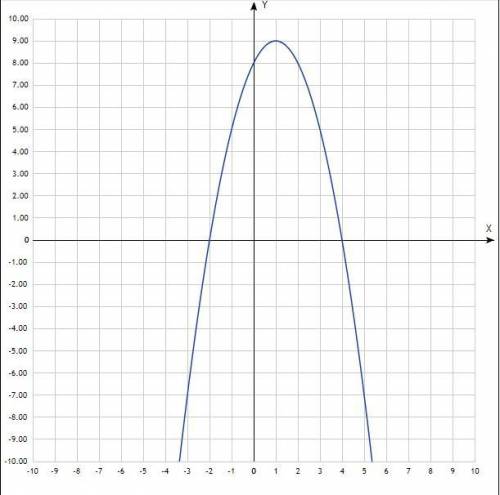
4) Построить график функции у = -х² + 2х + 8.
График функции - парабола со смещённым центром, ветви направлены вниз. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -3 -2 -1 0 1 2 3 4 5
у -7 0 -5 8 9 8 5 0 -7
Для точности построения найти координаты вершины параболы:
х₀ = -b/2a
x₀ = -2/-2
x₀ = 1;
y₀ = -(1)² + 2*1 + 8 = -1 + 2 + 8 = 9;
y₀ = 9;
Координаты вершины параболы (1; 9).
а) Согласно графика, наименьшего значения функции не существует.
Согласно графика, наибольшее значение функции = 9.
б) Область значений функции: у может быть любым, только меньше либо равен 9.
Запись: Е(у): у∈R : у <= 9.
в) Промежуток возрастания: х∈(-∞; 9];
Промежуток убывания: х∈([9; +∞).
г) f(x) < 0 при х∈(-∞; -2)∪(4; +∞).