
Сделаем замену
=
x2, тогда биквадратное уравнение примет вид
Для решения этого квадратного уравнения найдем дискриминант:
D = 22 - 4·1·(-4) = 20
x 2 = -2 - √20 2 x 2 = -2 + √20 2
x 1 = ( -2 + √20 )1/2 ≈ 1.1118 2 x 2 = -( -2 + √20 )1/2 ≈ -1.1118 2
а) прямая проходит через начало координат, т. е. через точку О (0;0), а также через точку А (0,6;-2,4). это значит что у=0 при х=0 и у=-2,4 при х=0,6. графиком функции является прямая. уравнение прямой - у=к*х осталось найти коэффициент к. -2,4 = (-4)*0.6 отсюда у=-4х б) прямая пересекает оси координат в точках В (0;4) и С (-2,5;0). получаем систему уравнений 4=0*к+а и 0=(-2.5)*к+а. из первого уравнения а=4 подставляем значение а во второе уравнение и рассчитываем к. в итоге получаем к=1,6. у=1.6х+4
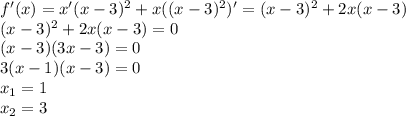
(х^+2x)=t
t^2-2t*3=0
t^2-6t=0
t(t-6)=0
t=0 t=6
1) t=0 x^2+2x=0
x(x+2)=0
x1=0 x2=-2
2)t=6
x^2+2x=6
x^2+2x-6=0
D=4+24=28
VD=V(4*7)=2V7
x3=(-2-2V7)/2=-1-V7
x4=-1+V7