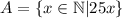
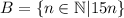
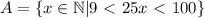
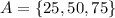
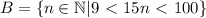
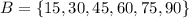
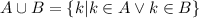- то есть, это такое множество всех k, так что, либо k в А либо в В, или в А и в В одновременно.
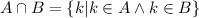- то есть, это такое множество всех k, так что, k и в А и в В одновременно.
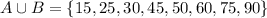- то есть, это множество всех чисел которые кратны либо 25 либо 15, или 25 и 15 одновременно.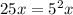
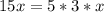
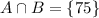
N2
а) 3x+12>0 3x>-12 x>-4
2x-3<0 2x<3 x<1,5 x∈(-4;1,5)
б) 3x+2>2x-3 x>-5
x-5>0 x>5 x∈(5;+∞)
N3
a)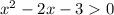 
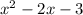=0
x1+x2=2 x1=3
x1
x2=-3 x2=-1
(x-3)(x+1)>0
+ +
_____._______._____
-1 - 3
x∈(-∞;-1)∪(3;+∞).
б)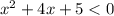 
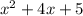=0
d=(4)²-415=16-20=-4
нет решений
в)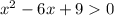 
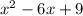=0
(x-3)²=0
(x-3)(x-3)>0
+
_____._____
3 - x∈(-∞;3)
1) 3x^2+x^3 x=0 x=-3
x=-3 точка минимума y(-3)=-27+81/4=-27/4
2) e^(-2x)-2e^(-2x)(x+1)=e^(-2x)-2xe^(-2x)-2e^(-2x)=-e^(-2x)(2x+1)
x=-1/2
- точка максимума производная меняет знак с + на -
y(-1/2)=1/2*e^1=e/2