x^2+7x=0 49-x^2=0 -6x^2=0 13-x^2=0
х(x+7)=0 -x^2=-49 х^2=0 -x^2=-13
x=0 x+7=0 x=корень из 49 x=0 x^2=13
x=-7 х=7 x=корень из 13
-x^2-25=0 x^2-100=0
-x^2=25 x^2=100
-x=корень из 25 x=корень из 100
-х=5 х=10
х=-5
рисунок сейчас приложу. Затем напишу решение, оно несложное.
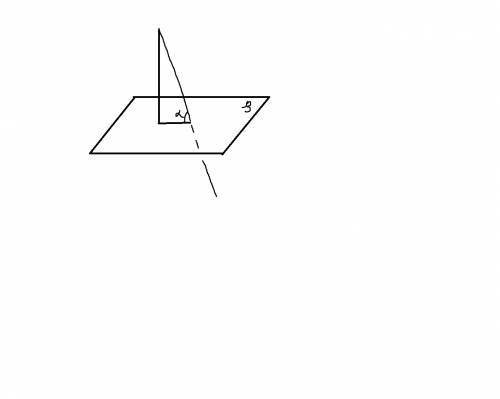
Углом между наклонной и плоскостью называется угол между наклонной и её проекцией на плоскость, что мы и можем видеть по рисунку. Рассмотрим прямоугольный треугольник. В нём роль перпендикуляра играет один из катетов(обозначим его a), а наклонная - его гипотенуза(назовём её c). По условию, b < c в два раза. Это означает, что b / c = 1/2. Но с другой стороны,
b / c = sin α(как отношение противолежащего катета к гипотенузе).Значит,
sin α = 1/2, отсюда α = 30° - это искомй угол
xy(xy+1-(x+y))=72
1+(x+y)+xy=20
x+y=t
xy=s
s(s+1-t)=72 s(s+1-19+s)=72 2s(s-9)=72 s^2-9s-36=0 s1=12 s2=-3
s+t=19 t=19-s t1=7 t2=22
x+y=7
xy=12 x=3 y=4
x=4 y=3
x+y=22
xy=-3 x3=11+2sqrt(31) y3=11-2sqrt(31)
x4=11-2sqrt(31) y4=11+2sqrt(31)