1)sin(x-pi/4)=0
t=x-pi/4
sint=0
1.t=0+2pi*k
x-pi/4=0
x=pi/4
2.t=pi+2pi*k
pi=x-pi/4
x=5pi/4+2pi*k
3)sinx(3x+pi/3)=1
t=3x+pi/3
sint=1
t=pi/2
3x+pi/3=pi/2
x=pi/18
5)tg(x-pi/6)=-√3
t=x-pi/6
tgt=-√3
t=-pi/3+2pi*k . k=Z
t=2pi/3+2pi*k . k=Z
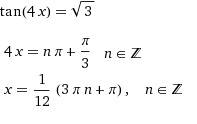
15
Объяснение:
x-скорость ветра
Летя за ветром, его скорость стала 45+х, а против 45-х. В обеих случаях он пролетел 120км и потратил на все это в сумме 6 часов. Ко времени, за которое он пролетел двигаясь по ветру, добавляем время за которое он пролетел, летя против ветра и получаем 6. Решаем уравнение отталкиваясь от формулы S/v=t:
120/(45+x) + 120/(45-x) = 6
((120(45-х)+120(45+х))/((45+x)(45-x))=6
(5400-120x+5400+120x)/(2025+45x-45x-x^2)=6
10800/(2025-x^2)=6
10800=6(2025-x^2)
10800=12150-6x^2
6x^2=12150-10800
6x^2=1350
x^2=225
x1=15
x2=-15
Скорость не может быть отрицательной, поэтому х=15
1)sin(x-π/4)=0
x-pi/4 = pi*k , k - Z
x=pi/4 +pi*k , k - Z
2)tg4x=√3
4x=pi/3 + 2*pi*k, k - Z
x=pi/12 * pi*k/2 , k - Z
3)sinx(3x+π/3)=1
3x+pi/3=pi/2+2*pi*k , k - Z
x=pi/18+2*pi*k/3 , k - Z
4)cos3x=1/2
3x=+-pi/3+2*pi*k , k - Z
x=+-pi/9+2*pi*k/3 , k - Z
5)tg(x-π/6)=-√3
x-pi/6=-pi/3+2*pi*k , k - Z
x=-pi/6 + 2*pi*k , k - Z