x = 5, y = 2
Объяснение:
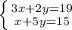
Метод сложения — это когда мы делаем так, чтобы можно было сократить одно из неизвестных в системе. То есть, нам нужно умножить одно из уравнений на такое число, чтобы при сложении с другим уравнением сократилось одно неизвестное (x или y)
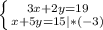
Я умножил нижнее уравнение на -3, потому что сверху у меня стоит неизвестное 3x, а чтобы его сократить, надо его сложить с -3x
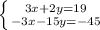
Складываем уравнения, то есть часть, находящуюся слева от равно первого уравнения прибавляем к левой части второго, так же и с правыми частями:
3x + 2y - 3x - 15y = 19 - 45
-13y = -26
y = 2
Подставляем полученный y в одно из уравнений, например, в первое:
3x + 2*2 = 19
3x = 15
x = 5
х∈(3, 4).
Объяснение:
Решить систему неравенств:
х>3
4-х>0
Первое неравенство:
х>3
Решения неравенства находятся в интервале от х=3 до + бесконечности.
х∈(3, +∞), это решение первого неравенства.
Неравенство строгое, скобки круглые.
Второе неравенство:
4-х>0
-x>-4
x<4 знак меняется
Решения неравенства находятся в интервале при х от - бесконечности до 4.
х∈(-∞, 4), это решение второго неравенства.
Неравенство строгое, скобки круглые.
Теперь нужно на числовой оси отметить оба интервала, чтобы найти пересечение, то есть, такое решение, которое подходит двум неравенствам.
Чертим числовую ось, отмечаем точки 3 и 4. Штриховка от точки 3 вправо до + бесконечности, от 4 влево до - бесконечности.
Пересечение х∈(3, 4), это и есть решение системы неравенств.
5x+6+x-3=5+x-4
5x+x-x=5-4-6+3
5x=-2
x=-0.4