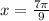По определению арифметической прогрессией является последовательность чисел в которой каждый последующий член начиная со второго получается прибавлением к предыдущему некоторого числа
пусть исходная последовательность
a, a+d, a+2d,
что если к каждому члену этой прогрессии прибавить одно и тоже число b, то получится последовательность
a+b, a+d+b, a+2d+b,
a+b, (a+b)+d, (a+b)+d,
получилась последовательность в которой первый член равен a+b а каждый последующий получается прибавлением d что по определению является арифметической прогрессией
Объяснение:
Відповідь:
1)(b-6)/(b-3)-b/(3-b)=2
2)(6с+4)/(7-с)+(3с+25)/(с-7)=-3
3)(3а+1)^2/(24a-24)+(a+3)^2/(24-24a)=(a+1)/3
4)(36-8x)/(x-6)^2-(4x-x^2)/(6-x)^2=1
Пояснення:
1)(b-6)/(b-3)-b/(3-b)=(b-6)/(b-3)+b/(b-3)=(2b-6)/(b-3)=2(b-3)/(b-3)=2
2)(6с+4)/(7-с)+(3с+25)/(с-7)=(3с+25)/(с-7)-(6с+4)/(с-7)=(3с+25-6с-4)/(с-7)=(-3с+21)/(с-7)=
(-3(с-7))/(с-7)=-3
3)(3а+1)^2/(24a-24)+(a+3)^2/(24-24a)=(9a^2+6a+1)/(24a-24)-(a^2+6a+9)/(24a-24)
=(9a^2+6a+1-a^2-6a-9)/(24a-24)=(8a^2-8)/(24(a-1))=(a^2-1)/(3(a-1))=(a-1)(a+1)/(3(a-1))
=(a+1)/3
4)(36-8x)/(x-6)^2-(4x-x^2)/(6-x)^2=(36-8x)/(x-6)^2-(4x-x^2)/(x-6)^2=(36-8x-4x+x^2)/(x-6)^2=
(x^2-12x+36)/(x-6)^2=(x-6)^2/(x-6)^2=1
Здесь применима формула двойного угла для косинуса.
Если обозначить выражение в скобках через t, то есть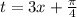 , то уравнение переписывается следующиим образом
, то уравнение переписывается следующиим образом
Воспользуемся формулой косинуса суммы углов
Заметим, что при k=6, корень уже не попадает в заданный промежуток![[\frac{3\pi}{4}; \pi]](/tpl/images/0120/4709/98547.png) ,
,
Докажем, что![\frac{7\pi}{9}\in [\frac{3\pi}{4};\pi]](/tpl/images/0120/4709/121d2.png)
То есть всего лишь один корень попадает в этот промежуток
ответ: при k=5