Question

Решить вот это: а) cos(5п/8)*cos(3п/8)+sin(5п/8)*sin(3п/8) б) sin(2п/15)*cos(п/5)+cos(2п/15)*sin(п/5) в) cos(п/12)*cos(п/4)-sin(п/12)*sin(п/4) г) sin(п/12)*cos(п/4)-cos(п/12)*sin(п/4) если у вас есть возможность объяснить как это делается, воспользуйтесь ей, ! я помню, что эти числа (п/4 и т.д.) как-то определяются по тригонометрическому кругу, но как! ? p.s. надеюсь на вашу совесть, , давая столько пунктов, что вы

Answer 1

по формулам синуса и косинуса суммы и разности двух аргументов имеем:

cos(5П/8)*cos(3П/8)+sin(5П/8)*sin(3П/8)=сos(5П/8-3П/8)=cos(П/4)=корень2/2

sin(2П/15)*cos(П/5)+cos(2П/15)*sin(П/5)=sin(2П/15+П/5)=sin(2П/15+3П/15)=sin(5П/15)=sin(П/3)=корень3/2

cos(П/12)*cos(П/4)-sin(П/12)*sin(П/4)=сos(П/12+П/4)=сos(П/12+3П/12)=сos(4П/12)=сos(П/3)=1/2

sin(П/12)*cos(П/4)-cos(П/12)*sin(П/4)=sin(П/12-П/4)=sin(П/12-3П/12)=sin(-2П/12)=sin(-П/6)=-sin(П/6)=-1/2

Answer 2

тут собрался коктейль формул косинуса разности и суммы, формулы синуса разности и суммы.

cos(α-β)=cosαcosβ+sinαsinβ

cos(α+β)=cosαcosβ-sinαsinβ

а) cos(5П/8)*cos(3П/8)+sin(5П/8)*sin(3П/8)=cos(5π/8-3π/8)=cos(2π/8)=cos(π/4)=1/√2

б) sin(2П/15)*cos(П/5)+cos(2П/15)*sin(П/5)=

=sin(2π/15+π/5)=sin(π/3)=√3/2

в) cos(П/12)*cos(П/4)-sin(П/12)*sin(П/4)=cos(π/12+π/4)=cos(π/3)=1/2

г) sin(П/12)*cos(П/4)-cos(П/12)*sin(П/4)

=sin(π/12-π/4)=sin(11π/6)=-1/2

========================================================

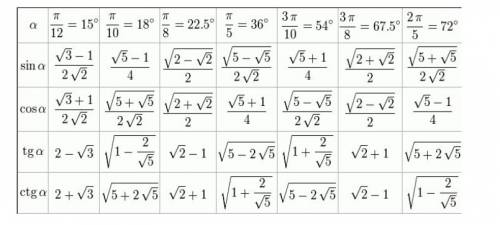
таблица нестандартных углов смотри во вложении!