1) 
Область определения
{ 3x - 4 > 0; x > 4/3
{ 12 - 5x > 0; x < 12/5
D(x): x ∈ (4/3; 12/5)
Так как основания логарифмов одинаковые, то и выражения под логарифмами равны.
3x - 4 = 12 - 5x
3x + 5x = 12 + 4
8x = 16; x = 2 ∈ (4/3; 12/5) - это решение.
2) 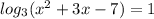
Область определения:
x^2 + 3x - 7 > 0
D = 3^2 - 4*1(-7) = 9 + 28 = 37
x1 = (-3 - √37)/2 ≈ -4,541; x2 = (-3 + √37)/2 ≈ 1,541
D(x) : x ∈ (-oo; (-3-√37)/2) U ((-3+√37)/2; +oo)
Логарифм - это показатель степени, в которую надо возвести основание, чтобы получить число под логарифмом.
x^2 + 3x - 7 = 3^1 = 3
x^2 + 3x - 10 = 0
(x + 5)(x - 2) = 0
x1 = -5 ∈ D(x); x2 = 2 ∈ D(x) - это два решения.
3) 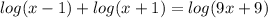
К сожалению, мы не знаем основание логарифма, но это неважно.
Главное, что основание должно быть везде одинаковое.
Область определения:
{ x > 1
{ x > -1
D(x) : x ∈ (1; +oo)
Решаем уравнение
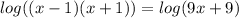
Так как основание везде одинаковое, можно перейти к выражениям
(x - 1)(x + 1) = 9x + 9 = 9(x + 1)
Так как x = -1 не может быть, то делим все на (x + 1)
x - 1 = 9
x = 10 - это решение.
11 частей за день съели. Осталось 5 кусочков.
Запишем количество съеденной пиццы в виде дроби — 11 8 .
На рисунке хорошо видно,
что 11 8 пиццы = 1 пицца + 3 8 пиццы,
или 11 8 пиццы = 8 8 пиццы + 3 8 пиццы
значит, 8 8 пиццы = 1 пицца.
Дроби, у которых числитель больше либо равен знаменателю
называются неправильные, а те у которых числитель меньше
знаменателя правильными.
Дроби 8 8 и 11 8 — неправильные,
они могут быть записаны другим
8 8 = 1, 11 8 = 1 + 3 8 .
Осталось — 5 8 пиццы.
5 8 — правильная дробь.
Сравним эти виды дробей с единицей.
Правильная — 5 8 < 1 .
Неправильная — 11 8 > 1 или 8 8 = 1 .
Обратите внимание, где расположены точки, отмеченные правильными
и неправильными дробями на координатном луче.
Правильная — 5 8 левее единицы.
Неправильная — 11 8 правее единицы
и 8 8 совпадает с единицей.