ответ: 3 км/ч
Пошаговое решение:
Пусть собственная скорость равна х км/ч, тогда скорость против течения равна (x-1) км/ч, а по течению — (x+1) км/ч. Время, затраченное против течения, равно 6/(x-1) ч, а по течению — 6/(x+1) ч. На весь путь байдарка затратила 6/(x-1) + 6/(x+1) ч, что по условию составляет 4ч30мин.
4 ч 30 мин = 4 ч+ 30/60ч = 4,5 ч.
Составим и решим уравнение:
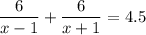
Для простоты умножим обе части уравнения на 2(x-1)(x+1)≠0
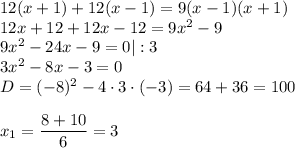
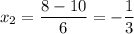- не удовлетворяет условию
Собственная скорость байдарки составляет 3 км/ч.
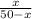, где х - вода, а (50-х) - кислота.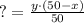
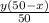- от II раза кислоты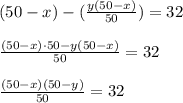
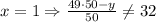
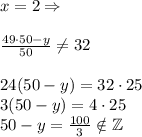
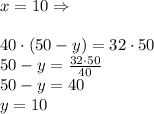
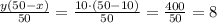литров кислоты
Пусть х - скорость каждой лодки,
а - скорость реки
За 3 часа первая лодка х-а)*3
Вторая х+а)*3
Известно, что:
(х+а)*3-(х-а)*3=13,2
Решаем:
Делим обе части уравнения на 3:
(х+а)-(х-а)=13,2/3=4,4
х+а-х+а=4,4
2а=4,4
а=4,4/2=2,2 км/ч
ответ: 2,2 км/ч