Пусть скорость течения реки (она же - скорость плота) равна r, скорость катера равна k.
За одно и то же время плот км, а катер - 96 км по течению и (96-24) = 72 км против течения.
Значит, 24/r = 96/(k+r) + 72/(k-r).
Сократим на 24: 1/r = 4/(k+r) + 3/(k-r).
Приведём правую часть к общему знаменателю:
1/r = (7k-r) / (k+r)(k-r).
Домножим на знаменатель (ведь он не равен нулю, иначе катер не смог бы плыть):
(k+r)(k-r) = (7k-r)*r.
kk - rr = 7kr - rr.
kk = 7kr.
k = 7r.
На 96 км по течению и 96 км против течения у катера ушло 14 часов.
Значит, 96/(k+r) + 96/(k-r) = 14.
Приводим к общему знаменателю:
96*2k / (k+r)(k-r) = 14.
(k+r)(k-r) = 96k/7.
kk - rr = 96k/7.
С учётом полученного соотношения k=7r, преобразуем:
49rr - rr = 96r.
48rr = 96r.
r = 2, тогда k = 14.
Проверяем.
Плот км за 24/2 = 12 часов.
Катер проплыл до места встречи за те же 96/16 + 72/12 = 12 часов.
Туда-обратно катер проплыл за 96/16 + 96/12 = 14 часов.
Пусть x - производительность первой трубы, y - производительность второй. Первая труба заполнит бассейн за 1/x часов, вторая "опустошит" - за 1/y часов. Известно, бассейн будет опустошаться на 3 часа дольше, чем наполняться, т.е.
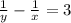
В то же время, если открыть обе трубы, то бассейн наполнится за 36 часов, т.е.
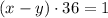
(здесь вычитание, т.к. трубы совершают противоположную работу - одна наполняет, вторая опустошает).
Имеем систему уравнений:
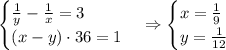
ответ: бассейн наполнится за 9 часов, вода полностью уйдёт за 12 часов.
2) 7 + 2i
3) 11 +3i +7 -2i = 18 +i
11+3i -7 +2i = 4 +5i
(11 +3i)(7 - 2i) = 77 +21i -22i - 6i^2= 77 -i +6 = 83 -i
(11 +3i) /(7 - 2i) = (11 +3i)(7 +2i)/(7-2i)(7+2i) = (77+21i+22i+6i^2)/(49 - 4i^2) = (71 +43i)/53 =
=71/53 + 43/53 i