Я не уверен, что правильно понял условие, но решу, так как понял:
1/3 (ква) * 0,5 (куб)
= Поскольку 2/9 это 1/3, то снизу и сверху сокращается и получается 0,5
2/9 (ква)
(куб) = 0,125
-1/2 (куб) * 2/3 (ква) - 1/8 * 4/9 - 1/18 49
= = = ___ = 2, 13/18
-1/7 (ква) -1/49 -1/49 18
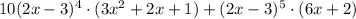
Объяснение:
Для начала необходимо понять, что данное выражение представляет собой произведение двух функций, а для производной от произведения функций существует правило:
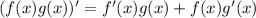
В данном случае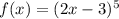 
, а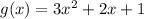 
Итак, нам потребуется производная от функции 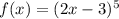, которая является сложной функцией, производная от которой берется по следующему правилу:
Здесь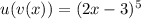 
, 
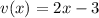
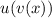- степенная функция, для нее правило такое:
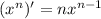
Вычисляем:
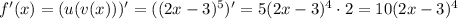
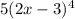мы получили, когда брали производную от внешней степенной функции , двойка появилась в результате взятия производной от 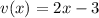. Т.е.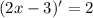 
---
Теперь возьмем производную от второго сомножителя в исходном выражении:
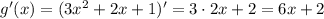
Подставляем все в формулу: ![\[(f(x)g(x))' = f'(x)g(x) + f(x)g'(x)\]](/tpl/images/1008/0917/ca526.png)
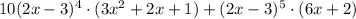
М*(х-2)=х^3-2x^2+x-2
М*(х-2)=х^2(x-2)+x-2
М*(х-2)=(x-2)(x^2+1)
M=x^2+1=(-2)^2+1=5
ответ:5