 ;
;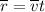 ;
;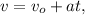 либо в векторном виде:
либо в векторном виде: 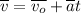 ;
;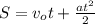 либо в векторном виде:
либо в векторном виде: 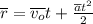 ;
;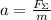 либо в векторном виде:
либо в векторном виде: 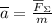 ;
; ;
;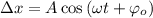 ;
;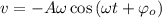 ;
; ;
;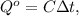 где
где 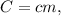 либо в удельном виде:
либо в удельном виде:  ;
;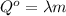 ;
;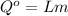 ;
; ;
; ;
;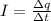 ;
;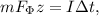 где
где  ;
;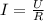 ;
;
 ;
; ;
; ;
;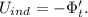
Для нахождения площади фигуры, ограниченной линиями функций у = х^2, у = 0 и х = 2 построим сначала графики этих функций. График функции у = 0 - прямая, которая задаёт ось ОХ; график функции х = 2 - прямая, параллельная оси ОУ и пересекающая ось ОХ в точке х =2. График функции у = х^2 - парабола, построена поточечно путём подбора значений координаты х и вычислением значения функции у в каждой такой точке. То есть:
1) х = -4, у = (-4)^2 = 16, на графике откладываем точки х = -4 и у = 16;
2) х = -3, у = (-3)^2 = 9, на графике откладываем точки х = -3 и у = 9;
3)х = -2, у = (-2)^2 = 4, на графике откладываем точки х = -2 и у = 4;
4)х = -1, у = (-1)^2 = 1, на графике откладываем точки х = -1 и у = 1;
5)х = 0, у = 0, на графике откладываем точки х = 0 и у = 0;
6)х = 4, у = 4^2 = 16, на графике откладываем точки х = 4 и у = 16;
7) х = 3, у = 3^2 = 9, на графике откладываем точки х = 3 и у = 9;
8)х = 2, у = 2^2 = 4, на графике откладываем точки х = 2 и у = 4;
9)х = 1, у = 1^2 = 1, на графике откладываем точки х = 1 и у = 0.
Заштрихованная на графике область является фигурой, площадь которой необходимо вычислить (площадь криволинейной трапеции). Вычисляется она по формуле определенного интеграла S = ∫f(x) dx - g(x) dx (верхний предел b, нижний предел a). Найдём верхний и нижний пределы интеграла. Для этого воспользуемся построенным графиком. Определим, на каком промежутке функция у = х^2 находится выше оси ОХ (так как значение площади не может быть числом отрицательным). Это отрезок [0;2], значит верхним пределом интеграла будет два (b = 2), нижним ноль (а = 0).
Вычислим определенный интеграл функции у = х^2 с пределами 2 и 0, значение которого и будет равно значению площади:
S = ∫(х^2)dx (верхний предел 2, нижний 0).
Интегрируем с формулы интегрирования:
∫х^ n dx = x^(n+1) / n+1,
и получаем выражение х^3/3.
Далее воспользуемся формулой Ньютона - Лейбница и получим значение площади, равное 8/3 или ~ 2,67 кв.ед.
ответ: площадь фигуры, ограниченной линиями у = х^2, х = 2, у= 0 равна 8/3 или ~ 2,67 кв.единиц.
Подробнее - на -
28:14=2незашто