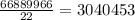
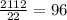
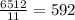
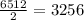
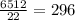
Рассмотрим теперь, сколько всего может быть чисел, удовлетворяющих нашему условию. Для этого разложим 60 на простые множители. 60=2·2·3·5. Это значит, что чисел, кроме: 1,2,3,4,5,6 в искомом числе быть не может. Докажем теперь, что в искомом числе не может быть цифры 3. Пусть искомое число содержит 3, тогда произведение оставшихся чисел равняется 20. А разбив 20 на простые множители, получим: 2²·5=20. Следовательно, оставшиеся цифры искомого числа: 1,2,4,5. Составим из оставшихся трех чисел число 20: 2·2·5 ; 4·5·1. Всего 2 варианта составления, без учета перестановок. А это означает, что искомое число не содержит число три: 1) 3+2 =5 , а 2+5≠ 5; 2) 3+5 =8, а 2+2≠8 ; 3) 3+1 = 4, а 4+5 ≠4 ; 4)3+5 =8, а 4+ 1≠ 5; 5) 3+4 = 7, а 5+1 ≠7. Из пунктов 1) - 5) можно сделать вывод, что если искомое число содержит 3, то оно не будет кратно 11, а значит и 22.
Докажем, что указанное число не содержит цифру 4. Если искомое число содержит цифру 4, то произведение оставшихся трех цифр равняется 15. Разложив число 15 на простые множители, убедимся, что: 15 = 3·5. А это означает, что искомое число содержит 3, что противоречит предыдущему доказательству.
У нас остались следующие числа для составления искомого числа: 1, 2, 5, и 6.
Рассмотрим теперь все оставшиеся варианты составления указанного числа: [1] если на первом месте (слева) стоит 1, то на третьем месте 6. Следовательно остается один вариант составления искомого числа 1562;
[2] если на первом месте (слева) стоит 2, то на третьем месте 5. Значит остается один вариант составления указанного в условии числа 2156;
[3] если же на первом месте (слева) стоит 5, то на третьем место цифра 2. А это значит, что у нас имеется всего один вариант для составления искомого числа: 5126.
[4] если на первом месте (слева) стоит 6, то на третьем место будет стоять 1, что означает, что у нас остался последний вариант составления искомого числа: 6512.
С пунктов [1] - [4] придем к заключению: можно составить лишь четыре числа, которые будут удовлетворять условию задачи, а именно: 1562, 2156, 5126, 6512.
ответ: 0,02; 0,32; 0,216.
Объяснение:
№ Д4.10.
Пусть событие А заключается в том, что объём воды в случайно выбранной бутылке отличается от нормы не более чем на 0,2 л, а событие В - более чем на 0,2 л. Фактически нам нужно найти вероятность события В р(В). По условию, вероятность события А р(А)=0,98. Так как события А и В несовместны и притом образуют полную группу событий, то р(А)+р(В)=1. Отсюда р(В)=1-р(А)=1-0,98=0,02. ответ: 0,02.
№ Д4.11.
Пусть событие А заключается в том, что школьнику достанется задача на тему "формулы приведения", а событие В - в том, что ему достанется задача на тему "универсальная тригонометрическая подстановка", а событие С - в том, что достанется задача на одну из этих тем. Тогда С=А+В, а так как события А и В несовместны, то р(С)=р(А)+р(В)=0,24+0,08=0,32. ответ: 0,32.
№ Д4.12.
Пусть событие А1 заключается в том, что занят первый оператор, событие А2 - второй, событие А3 - третий, а событие В - что заняты все три оператора. Тогда В=А1*А2*А3, а так как по условию события А1, А2 и А3 независимы, то р(В)=р(А1)*р(А2)*р(А3). По условию, р(А1)=р(А2)=р(А3)=0,6, и тогда р(В)=0,6*0,6*0,6=0,216. ответ: 0,216.