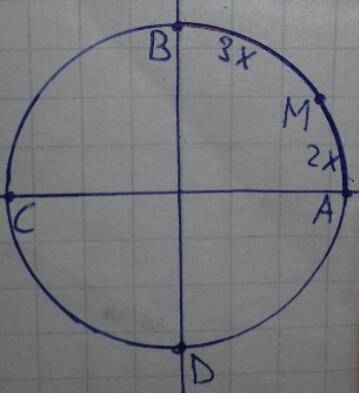
Дугу можно измерять угловой мерой (размер центрального угла, опирающего на дугу) или длиной (угловая мера умноженная на радиус). Числовая окружность имеет радиус 1, поэтому значение угловой меры численно равно значению длины.
Половина окружности это π и это же длина дуги (для числовой окружности).
∪AC = π = 2·∪AB ⇒ ∪AB = 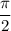
Пусть ∪AM =  , тогда ∪MB =
, тогда ∪MB = 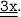
Т.к. первая четверть это ∪AB.
∪AM + ∪MB = 2x+3x = 5x = 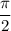 ⇒
⇒
x = 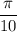 ⇒
⇒ 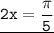 ;
; 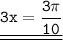
∪DM = ∪DA + ∪AM = 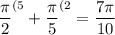
∪MC = ∪MB + ∪BC = 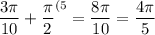
ответ: длина ∪AM = 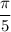
длина ∪MB = 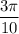
длина ∪DM = 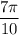
длина ∪MC = 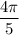
y=ax^2+bx+c,
x0=-b/(2a),
y0=c-b^2/(4a) или y0=f(x0)
1.1) y=x^2-4x+3,
x0=-(-4)/(2*1)=2,
y0=3-(-4)^2/(4*1)=-1, {или y0=2^2-4*2+3=-1}
a=1>0 - ветви параболы направлены вверх;
1.4)y= -x^2+6x-8,
x0=-6/(2*(-1))=3,
y0=-8-6^2/(4*(-1))=1;
a=-1<0 - ветви параболы направлены вниз;
2.1) |x^2+5|=6x,
x^2+5=6x,
x^2-6x+5=0,
по теореме обратной к теореме Виета:
x1=1, x2=5;
или
x^2+5=-6x,
x^2+6x+5=0,
по теореме обратной к теореме Виета:
x1=-5, x2=-1;
2.2)|x^2+x|+3x=5,
|x^2+x|=5-3x,
x^2+x=5-3x,
x^2+4x-5=0,
по теореме обратной к теореме Виета:
x1=-5, x2=1;
или
x^2+x=-(5-3x),
x^2+x=-5+3x,
x^2+2x+5=0,
D=b^2-4ac=2^2-4*1*5=4-20=-16<0,
нет решений;
2.3) (x+3)^4-13(x+3)^2+36=0,
(x+3)^2=t,
t^2-13t+36=0,
по теореме обратной к теореме Виета:
t1=4,t2=9;
(x+3)^2=4,
x^2+6x+9=4,
x^2+6x+5=0,
по теореме обратной к теореме Виета:
x1=-5, x2=-1;
или
(x+3)^2=9,
x^2+6x=0,
x(x+6)=0,
x3=0, или x+6=0, x4=-6;
3) 3x^2-7x+2<0,
3x^2-7x+2=0,
D=25,
x1=1/3, x2=2,
(x-1/3)(x-2)<0,
1/3<x<2,
xЄ(1/3;2)
-a+5b=7, a+2b=7
-a+5b +a+2b = 14
7b=14, b=2
a=7 - 2b, a= 7 -4, a=3
3x+2y-7=0