№1
1) a¹³*a⁻¹⁶=a¹³⁽⁻¹⁶⁾ = a¹³⁻¹⁶=a⁻³
-3⁻³ = 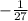
2) a⁻⁹:a⁻⁸=a⁻⁹⁻⁽⁻⁸⁾ = a⁻⁹⁺⁸ = a⁻¹
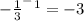
3) (a⁻²)¹¹*a²⁰= a⁽⁻²⁾°¹¹ * a²⁰ = a⁻²² * a²⁰ = a⁻²²⁺²⁰= a⁻²
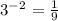
1 - Б
2 - А
3 - В
№2
График, думаю, сами легко построите.
y = 8/x
1) Значение функции, если x = -4
y = 8/-4 = -2
2) Значение аргумента, если y = 1
x = 8/y
x = 8/1 = 8
3) Аргумент принимает отрицательные значения, если x ∈ (-∞, 0)
№3
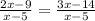
______
Область допустимых значений (Условие):
x-5 ≠ 0
x ≠ 5
_______
Если знаменатели равны, то и числители тоже равны.
2x -9 = 3x - 14
2x - 3x = -14 + 9
-x = -5
x = 5 - не подходит по ОДЗ
x ∈ ∅
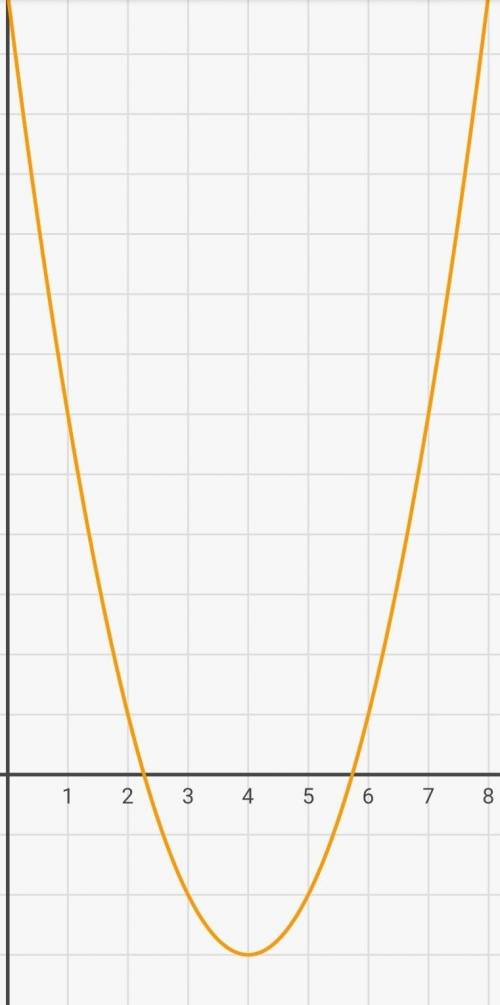
а) f(1,5)=3,25
если подставить вместо икса в формулу графика 1,5 получим 3,25.
ㅤ
б) подставим вместо "у" 2, решим полученное уравнение:
х²-8х+13=2
х²-8х+13-2=0
х²-8х+11=0
х1=1.75; х2=6,25.
(С округлением)
Решив квадратное уравнение мы получили корни. эти корни и есть точки, при которых у=2.
f(1.75)=2; f(6.25)=2.
ㅤ
в) x=0 в точках: (2.25;0) и (5.75;0)
г) убыв на хє(-∞;4]
Пояснения:
а) значение у при х = 1,5. Цифра по ОсиY в точке где х=1,5, у нас это 3,25.
б) значения х, при которых у = 2 Цифра по Оси Х, где по Оси у =2. у нас это 1,75.
Можно получить эти значения подставив вместо "у" 2, и решив уравнение.
в) нули функции. Точки где график пересекает Ось Х, или точка где х=0.
г) промежуток, в котором функция убывает. промежуток когда функция идёт вниз- называется промежутком убывания функции, и когда идет на верх- промежутком возрастания.
а) (2m)^2 + 2m + 1 = 4m^2 + 2m + 1 = 2(2m^2+m) + 1, где 2m^2+m натуральное (в силу того, что произведение и сумма натуральных числе всегда натуральна), будет нечётным.
(2m+1)^2 + (2m+1) + 1 = 4m^2 + 4m + 1 + 2m + 1 + 1 = 4m^2 + 6m + 2 + 1 =
2(2m^2 + 3m + 1) + 1, где 2m^2 + 3m + 1 натуральное, будет нечётным.
b) Квадрат чётного числа - чётный. Потому число n^2 + n + 1 не может быть квадратом чётного числа.
Покажем, что число не может быть и квадратом нечётного числа:
n^2 + n + 1 = n^2 + 2n + 1 - n = (n+1)^2 - n
Т.е. число n^2 + n + 1 отличается от квадрата (n + 1)^2 на n единиц. Может ли такое число быть квадратом?
(n + 1)^2 - n^2 = n^2 + 2n + 1 - n^2 = 2n + 1 > n
Не может.
Цельная и стройная запись решения:
n^2 < n^2 + n + 1 = (n + 1)^2 - n < (n + 1)^2
Т.к. число n^2 + n + 1 лежит между двумя квадратами последовательных натуральных чисел, само оно не может быть квадратом натурального числа.