1. Будем доказывать методом математической индукции.
Проверяем истинность утверждения при n = 1:
а) 2*49 + 16 + 40 = 154 = 11*14 - делится на 11.
б) Предположим, что 2*7^(2k) + 16^k +8*5^k - делится на 11. Где k - произвольное натуральное число.
в) Докажем, что тогда при n = k+1 полученное выражение - тоже делится на 11:
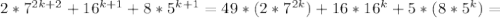
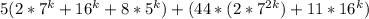
Теперь четко видно что оба больших слагаемых делятся на 11:
первое - исходя из предположения, второе - имеет 11 как общий сомножитель для своих слагаемых.
Итак мы доказали , что если при произвольном n= k выражение делится на 11, то и при n = k+1 выражение делится на 11.
Значит исходное выражение делится на 11. что и требовалось доказать.
2)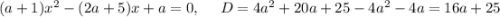
D>0 a>-25/16 a>-1,5625
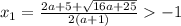
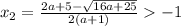
Разбиваем ОДЗ на две части:
а) (-1; беск)
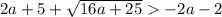
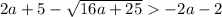
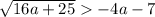
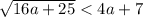
Первое из написанных неравенств верно. Проверим второе:
16a+25<16a^2+56a+49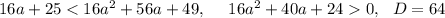
Корни -1; -1,5 Решение с учетом ОДЗ: (-1; беск)
б) (-1,5625; -1)
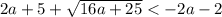
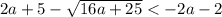
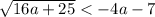
Правая чать на выбранной области - отрицательна, что недопустимо. Здесь решений нет.
ответ: (-1; бескон).
3.
![[\sqrt{1-sin^2153}+\sqrt{tg^2207-sin^2207}]sin63=[-cos153+\frac{sin^2207}{-cos207}]sin63](/tpl/images/0025/6265/72073.png)
![=[sin63+\frac{cos^263}{sin63}]sin63=sin^263+cos^263=1](/tpl/images/0025/6265/378ae.png)
ответ: 1
2^(2x-x²) *2^(-1) +1 /(2^(2x -x²) -1) -2 ≤ 0 ;
Производя замену t = 2^(2x -x²) >0 , получаем :
t /2 +1/(t -1) -2 ≤ 0 ;
( t(t-1) +2 - 4(t -1) ) / 2(t-1) ≤ 0 ;
(t² -5t +6)/(t-1) ≤ 0 ;
(t-2)(t-3)/(t-1) ≤ 0 ;
- + - +
(1) [2] [3]
t ∈(0 ;1) U [2 ; 3] .
[ 2^(2x -x²) < 1 ; 2 ≤ 2^(2x -x²) ≤3 .
[ 2x -x² < 0 ; 1 ≤ 2x -x² ≤ Loq_2 3.
[ x(x-2) >0 ; { x² - 2x +1≤0 ; x² -2x + Loq_2 3 ≥0 .
[ x(x-2) >0 ; { (x- 1)² ≤0 ; (x -1)² +( Loq_2 3 -1) ≥0 .
* * * Loq_2 3 -1 > Loq_2 2 -1 =0 * * *
[ x∈(-∞;0) U(2 ;∞) ; { x =1 ; -∞ < x < ∞ .
[ x∈(-∞;0) U(2 ;∞) ; x =1 .
ответ : x ∈ (-∞;0) U {1} U (2 ;∞).