Question

Разделить 4500 на три части так, чтобы 80% первой, 53 1/3 % второй и 40% третьей чати были равны между собой. плз, !

Answer 1

$4500=a+b+c$

Запишем условие задачи, переведя его на язык математики:

80% от а = 0,8а

40% от с = 0,4с

53 1/3% от в =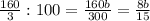 $\frac{160}{3}:100=\frac{160b}{300}=\frac{8b}{15}$

Получаем 0,8а=8в/15=0,4с

0,8а=0,4с, следовательно а=(0,4с):0,8=с/2

8в/15=0,4с или 8в/15=2/5с, следовательно в=(2с*15)/(5*8)=3с/4

По условию, а+в+с=4500. Подставим в это уравнение найденные значения:

$\frac{c}{2}+\frac{3c}{4}+c=4500$

$\frac{2c+3c+c}{4}=4500|*4$

$9c=18000$

$c=2000$

$a=\frac{c}{2}=\frac{2000}{2}=1000$

$b=\frac{3c}{4}=\frac{3*2000}{4}=1500$

Проверка: 1000+1500+2000=4500