Найдем вероятность того, что у определенного работника взятая деталь стандартная (как отношение соответствующего числа стандартных деталей к общему числу деталей):
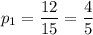
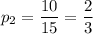
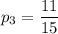
Поскольку события выбора по одной детали у каждого из работников независимы, то вероятность выбора у всех рабочих стандартных деталей определяется произведением вероятностей:
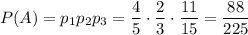
Найдем вероятности выбора нестандартных деталей у каждого работника:
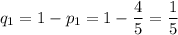
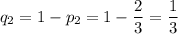
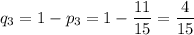
Одна стандартная деталь может быть выбрана только у первого работника, только у второго или только у третьего. Вероятность каждого из событий находится как произведение одной вероятности выбора стандартной детали на две другие вероятности выбора нестандартных деталей. Поскольку такие события несовместны, то полученные вероятности необходимо сложить.
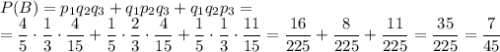
ответ: А) 88/225; Б) 7/45
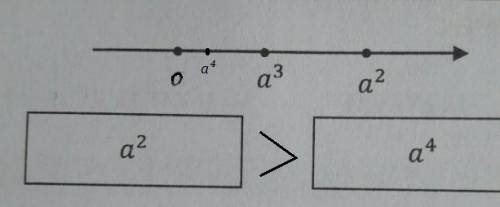
ответ: а² > a⁴ .
Объяснение:
Так как на чертеже а² лежит на оси правее, чем а³ , то а² > а³ .
А это значит, что число "а" находится в пределах от 0 до 1: 0<a<1 .
Если , например, а=0,1 , то а²=0,01 , а³=0,001 , a⁴=0,0001 , то есть 0,0001<0,001<0,01<0,1 ⇒ a⁴ < a³ < a² < a .
Значит, и более старшие степени числа "а" будут давать меньшие значения. То есть а⁴ < a²
Для сравнения, если a>1 , то a⁴>a³>a²>a . Например, а=3 , тогда a⁴=81 , а³=27 , а=9 .
P.S. Самая крайняя левая точка на чертеже - это 0 , а не а .
х^2+(x+1)^2=85
x^2+x^2+2x+1=85
2x^2+2x-84=0
х=-7
одно число -7
второе -6