0×Х=0
это уравнение не имеет корней
№1
а) √50 > 7
√50 > √7²
√50 > √49
б) 4√6 > 3√7
√4²*6 > √3²*7
√16*6 > √9*7
√96 > √63
№2
а) √(196 * 0,64) = √(14²*(0,8)²) = 14 * 0,8 = 11,2
б) √(72*0,5)=√36=√6² = 6
в) 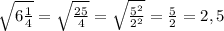
г) √(-2)⁶ = √((-2)³)²=(-2)³= - 8
№3
а) (√3+√2)² = (√3)²+ 2 *√3*√2 + (√2)²= 3 + 2√6 + 2 = 5 +2√6
б) (4 - √5)(4 + √5) = 4² - (√5)² = 16 - 5 = 11
в) 5√12 - 2√27 - 3√3 = 5√(4*3) - 2√(9*3) - 3√3 = 5√(2²*3) - 2√(3²*3) - 3√3 = 5*2√3 - 2*3√3 - 3√3= 10√3 - 6√3 - 3√3 = √3
№4
√(72*а⁵) = √(36*2 * а⁴*а)= √(6²*2 * (а²)² * а) = 6*а²*√(2а)
№5
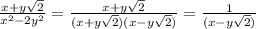
№6
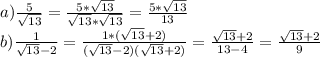
Данный многочлен можно разложить на множители группировки. Сгруппируем 1 и 2, 3 и 4 множители и выпишем их в отдельных скобках:
(bm+3b)+(2cm+6c). Теперь, из каждой скобки вынесем общий множитель. В 1 скобке это b, а во 2 - 2с. Вынесем данные множители и получим:
b(m+3)+2c(m+3). Теперь общее выражение m+3 вынесем в скобках отдельно, а остальное запишем в других скобках:
(m+3)(b+2c). Это наше разложение, оно является ответом.
Оформление в тетради должно выглядеть так:
bm+3b+2cm+6c=b(m+3)+2c(m+3)=(m+3)(b+2c).
0*х=10 - это уравнение не имеет корней, потому что при умножении любого числа на 0 будет 0, то есть 10 в произведении мы никогда не получим, х=∅(х равен пустому множеству).