1) х₁=0, х₂=5, х₃=-5
2) х=1/12
3) х₁=3, х₂=4, х₃=-4.
Объяснение:
1) 4x³-100x = 0
Выносим общий множитель - 4х - за скобки.
4х(х²-25)=0
Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.
4х=0
х=0
х²-25=0
х²=25
х=±√25
х=±5
ответ: х₁=0, х₂=5, х₃=-5.
2) 144x^3-24x^2+x=0
Выносим общий множитель - х - за скобки.
х(144х²-24х+1)=0
х=0
144х²-24х+1=0
Квадратное уравнение решаем через дискриминант.
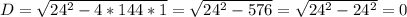
Уравнение будет иметь один корень, т.к. дискриминант равен нулю.
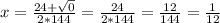
ответ: х=1/12.
3) x³-3x²-16x+48=0
Сгруппируем.
(х³-3х²)+(-16х+48)=0
Из первой скобки вынесем общий множитель х², а из второй (-16).
х²(х-3)-16(х-3)=0
Вынесем за скобки общий множитель (х-3).
(х-3)(х²-16)=0
х-3=0
х=3
х²-16=0
х²=16
х=±√16
х=±4
ответ: х₁=3, х₂=4, х₃=-4.
При имеющихся исходных данным возможно 2 ответа:
1) b₁ = 6; q = 1/4;
1) b₁ = -6; q = -1/4;
Объяснение:
Член геометрической прогрессии с номером n вычисляется по формуле
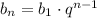
b₄ - b₂ = b₁ · q³ - b₁· q = b₁q(q² - 1)
b₆ - b₄ = b₁ · q⁵ - b₁· q³ = b₁q³(q² - 1)
По условию
b₁q(q² - 1) = -45/32 (1)
b₁q³(q² - 1) = -45/512 (2)
Преобразуем выражение (2)
b₁q³(q² - 1) = b₁q(q² - 1) · q²
В численном виде это можно записать как
-45/512 = -45/32 · q²
Откуда
q² = -45/512 : (-45/32)
q² = 1/16
q = ±1/4
Подставим q = 1/4 в выражение (1)
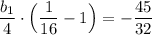
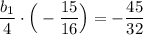
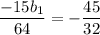
0.5b₁ = 3
b₁ = 6
Подставим q = -1/4 в выражение (1)
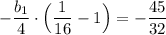
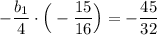

0.5b₁ = -3
b₁ = -6
Проверка:
1) b₁ = 6; q = 1/4
b₂ = 6 · 1/4 = 3/2
b₄ = 6 · 1/64 = 3/32
b₄ - b₂ = 3/32 - 3/2 = -45/32
b₆ = 6 · 1/1024 = 3/512
b₆ - b₄ = 3/512 - 3/32 = -45/512
2) b₁ = -6; q = -1/4
b₂ = -6 · (-1/4) = 3/2
b₄ = -6 · (-1/64) = 3/32
b₄ - b₂ = 3/32 - 3/2 = -45/32
b₆ = -6 · (-1/1024) = 3/512
b₆ - b₄ = 3/512 - 3/32 = -45/512
1. 6x^2+x-1=0
Дискриминант: D = b2 - 4a*c = 12- 4*6*-1 = 25
Если D>0 то уравнение имеет 2 вещественных корня:
x1 = (-b+√D) /2а= (-1+√ 25)/12 =0.4
x2 = (-b-√D)/2а = (-1-√ 25)/12 =-0.5
2.2 x2 - 5 x + 3 = 0
2 x2 -5 x + 3= 0
2 x2 -5 x + 3= 0
Дискриминант: D = b2 - 4a*c = -52- 4*2*3 = 1
Если D>0 то уравнение имеет 2 вещественных корня:
x1 = (-b+√D)/2а = (5+√ 1)/4 =1.5
x2 = (-b-√D)/2а = (5-√ 1) /4=1