На 1 месте может быть любая цифра от 1 до 9, то есть 9 вариантов.
Н 2, 3, 4 и 5 месте - любая от 0 до 9, то есть по 10 вариантов.
Всего 9*10*10*10*10 = 90 000 вариантов.
а) Все цифры разные. На 1 месте может быть любая цифра от 1 до 9 - 9 вариантов.
На 2 месте может быть 0 и любая из 8 других цифр, но не та, которая на 1 месте. - 9 вариантов.
На 3 месте может быть любая из 8 оставшихся цифр. На 4 - любая из 7, на 5 - любая из 6.
Всего 9*9*8*7*6 = 27216 вариантов. Вероятность равна 27216/90 000 = 0,3024
б) Все цифры одинаковые - таких вариантов всего 9, от 11111 до 99999. Вер-сть 1/10 000 = 0,0001
в) Все цифры нечетные На каждом месте может быть одна из 5 цифр - 1,3,5,7,9.
Всего 5*5*5*5*5 = 3125 вариантов. Вероятность равна 3125/90 000 = 0,03472
2)Из обеих урн достают по одному шару.
Какова вероятность, что они будут одного цвета?
5/24*10/24 + 11/24*8/24 + 8/24*6*24 = 31/96 = 32.3%
ответ : 32.3%
3) ПО ОПРЕДЕЛЕНИЮ вероятность это отношение числа нужных вариантов к общему числу вариантов (какого-то события). То есть 2*9!/10! = 1/5;
4)Где-то 50 процентов
Дальше я хз
Объяснение:
5.
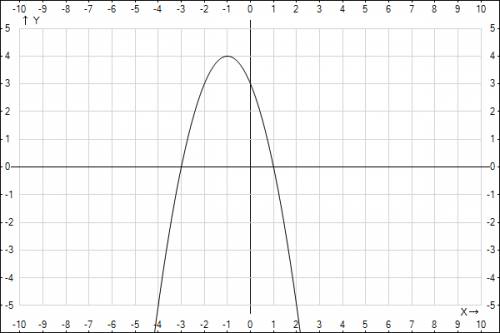
y=-x^2-2x+3,
a=-1<0 - ветви параболы вниз;
x_0=-b/(2a)=-(-2)/(2*(-1))=-1,
y_0=-(-1)^2-2*(-1)+3=4,
(-1;4) - вершина параболы;
x=0, y=3,
(0;3) - пересечение с Оу,
y=0, -x^2-2x+3=0,
x^2+2x-3=0,
по теореме Виета x_1=-3, x_2=1,
(-3;0), (1;0) - пересечения с Оx;
1) E_y=(-∞;4);
2) x∈(-1;+∞);
6.
(х^2+2х+1)(х^2-6х-16)<0,
(х^2+2х+1)(х^2-6х-16)=0,
х^2+2х+1=0, (x+1)^2=0, x+1=0, x=-1;
х^2-6х-16=0, по теореме Виета x_1=-2, x_2=8; х^2-6х-16=(x+2)(x-8);
(x+1)^2(x+2)(x-8)<0,
(x+1)^2≥0, x∈R,
(x+2)(x-8)<0,
-2<x<8,
x∈(-2;8);
7.
x^2-6bx+3b=0,
D<0,
D/4=k^2-ac=(-3b)^2-3b=3b^2-3b=3b(b-1),
3b(b-1)<0,
3b(b-1)=0,
b_1=0, b_2=1,
0<b<1,
b∈(0;1);
8.
ΔABC, уг.C=90°, CE - высота, AE=16см, BE=9см;
AB=AE+BE (по свойству сложения отрезков),
AB=16+9=25см;
AC^2=AB*AE (катет есть среднее геометрическое гипотенузы и смежного сегмента),
AC^2=25*16=400, AC=20см,
BC^2=AB*BE=25*9=225, BC=15см,
P=AB+AC+BC=25+20+15=60см.