Объяснение:
Для того чтобы показать, что число является составным достаточно показать, что оно у него есть делители помимо 1 и самого себя. Для начала надо понять на какое число заканчивается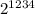 
. Для этого нужно понять на какую цифру заканчиваются степени двойки:
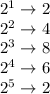
Таким образом последняя цифра в степенях двойки может быть только из множества {2, 4, 8, 6}, которое будет циклически повторяться. Дальше надо понять остаток от деления 1234 на 4. 1234 : 4 = 308 и остаток 2. Значит последния цифра у нас совершит 308 полных циклов и еще 2 шага. Таким образом число 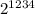заканчивается на цифру 4. Следовательно 
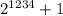заканчивается на цифру 5, а значит это число делится на 5 и как факт является составным.
На самом деле все очень просто! Сейчас расскажу.
Объяснение:
Здесь просто решаем многочлен, так как под формулу сокр. умножения он не подходит. То бишь:
1)=2а×5а - 2а×2в(первое число из первой скобки на другую скобу умножили, делаем дальше) +5в×5а - 5в×2в(второе число из первой скобки умножили на вторую скобку, со знаками вы уже должны сами разобраться) =10а^2 - 4ав + 25ва - 10в^2. Теперь мы видим 2 одночлена у которых одинаковая буквенная часть, то бишь - 4ав и +25ва. Значит их мы решаем: - 4ав +25ав =21ав(положительное число). Теперь приводим к многочлен стандартного вида:10а^2 + 21ав - 10в^2. Все, проще простого, если что то непонятно - пиши в комменты. Остальные примеры аналогичны.
