Алгебра: Выполните умножение: (7 класс ) (а+3)(а-4)=? (а-1)(6-а) =? (-а-1)(а+7)=? (5+а) (-2-а) =?

Выполните умножение: (7 класс ) (а+3)(а-4)=? (а-1)(6-а) =? (-а-1)(а+7)=? (5+а) (-2-а) =?

👇

Ответ:

natalyakulesch

30.05.2021

Принимайте решение=)))) )))) ))))
Выполните умножение: (7 класс ) (а+3)(а-4)=? (а-1)(6-а) =? (-а-1)(а+7)=? (5+а) (-2-а) =?

4,6(92 оценок)

Открыть все ответы

Ответ:

nastyapuhova1

30.05.2021

На заводе производится сплав, в котором на 2 кг алюминия приходится 1 кг никеля. 2 + 1 = 3 кг сплава.

Первая шахта: 60 рабочих; 5 рабочих часов в день;
2 кг алюминия или 3 кг никеля 1 рабочий за 1 час.
Общее количество рабочих часов в день: 60*5 = 300 часов.
1 час / 3 кг = 1/3 часа нужно, чтобы один рабочий добыл 1 кг никеля.
Для 3 кг сплава требуется
1/3 часа на добычу 1 кг никеля и
1 час на добычу 2 кг алюминия.
1 час + 1/3 часа = $1 \frac{1}{3} = \frac{4}{3}$ часа.

Пропорция
$\frac{4}{3}$ часа - 3 кг сплава
300 часов - Х кг сплава
$X = 300*3: \frac{4}{3} =900* \frac{3}{4} =675$ кг сплава
------------------------------------------
Вторая шахта: 260 рабочих, 5 рабочих часов в день,
3 кг алюминия или 2 кг никеля 1 рабочий за 1 час.
Общее количество рабочих часов в день: 260*5 = 1300 часов.
1 час / 2 кг = 1/2 часа, чтобы один рабочий добыл 1 кг никеля.
1 час / 3 кг = 1/3 часа, чтобы один рабочий добыл 1 кг алюминия.
Для 3 кг сплава требуется
1/2 часа для добычи 1 кг никеля и
1/3 часа * 2 кг = 2/3 часа для добычи 2 кг алюминия.
1/2 часа + 2/3 часа = $\frac{3+4}{6} = \frac{7}{6}$ часа.

Пропорция
$\frac{7}{6}$ часа - 3 кг сплава
1300 часов - Х кг сплава
$X = 1300*3: \frac{7}{6} =3900* \frac{6}{7} =3342 \frac{6}{7}$ кг сплава

Обе шахты могут обеспечить завод металлом для получения
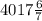$675 + 3342 \frac{6}{7}=4017 \frac{6}{7}$ кг сплава

ответ: $4017 \frac{6}{7}$ кг сплава.

4,7(38 оценок)

Ответ:

historican

30.05.2021

решения системы подстановки алгебраического сложения.

Алгоритмы и примеры решения системы уравнений:

Алгоритм решения системы линейных уравнений подстановки:

1. Выбрать одно уравнение (лучше выбирать то, где числа меньше) и выразить из него одну переменную через другую, например, Х через У. (можно и У через Х) . 2. Полученное выражение подставить вместо соответствующей переменной в другое уравнение. Таким образом, у нас получится линейное уравнение с одной неизвестной. 3. Решаем полученное линейное уравнение и получаем решение. 4. Подставляем полученное решение в выражение, полученное в первом пункте, получаем вторую неизвестную из решения. 5. Выполнить проверку полученного решения.

Пример

Решить систему уравнений: {Х+2*У =12{2*Х-3*У=-18

Решение: 1. Из первого уравнения данной системы выражаем переменную Х. Имеем Х= (12 -2*У) ; 2. Подставляем это выражение во второе уравнение, получаем 2*Х-3*У=-18; 2*(12 -2*У) – 3*У = -18; 24 – 4*У– 3*У = -18;

3. Решаем полученное линейное равнение: 24 – 4У – 3*У =-18; 24-7*У =-18; -7*У = -42; У=6;

4. Подставляем полученный результат в выражение, полученное в первом пункте. Х= (12 -2*У) ; Х=12-2*6 = 0; Х=0;

5. Проверяем полученное решение, для этого подставляем найденные числа в исходную систему. {Х+2*У=12;{2*Х-3*У=-18;{0+2*6 =12;{2*0-3*6=-18;{12 =12;{-18=-18;

Получили верные равенства, следовательно, мы правильно нашли решение.

ответ: (0,6)

Алгоритм решения алгебраического сложения

Алгоритм решения системы линейных уравнений с двумя неизвестными сложения.

1. Если требуется, путем равносильных преобразований уравнять коэффициенты при одной из неизвестных переменных в обоих уравнениях. 2. Складывая или вычитая полученные уравнения получить линейное уравнение с одним неизвестным 3. Решить полученное уравнение с одним неизвестным и найти одну из переменных. 4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную. 5. Сделать проверку решения.

Пример решения алгебраического сложения

Для большей наглядности решим сложения следующую систему линейных уравнений с двумя неизвестными:

{3*Х + 2*У = 10;{5*Х + 3*У = 12;

Так как, одинаковых коэффициентов нет ни у одной из переменных, уравняем коэффициенты у переменной у.

Для этого умножим первое уравнение на три, а второе уравнение на два.

{3*Х+2*У=10 |*3{5*Х + 3*У = 12 |*2

Получим следующую систему уравнений: {9*Х+6*У = 30;{10*Х+6*У=24;

Теперь из второго уравнения вычитаем первое.

Приводим подобные слагаемые и решаем полученное линейное уравнение. 10*Х+6*У – (9*Х+6*У) = 24-30; Х=-6;

Полученное значение подставляем в первое уравнение из нашей исходной системы и решаем получившееся уравнение. {3*(-6) + 2*У =10;{2*У=28; У =14;

Получилась пара чисел Х=6 и У=14.

Проводим проверку.