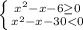
1) x² - x - 6 ≥ 0
(x - 3)(x + 2) ≥ 0
+ - +
______[- 2]______[3]_______
////////////// ////////////////
x ∈ (- ∞ ; - 2] ∪ [3 , + ∞)
2) x² - x - 30 < 0
(x - 6)(x + 5) < 0
+ - +
_______(- 5)______(6)______
///////////////////
x ∈ (- 5 ; 6)
Окончательно :
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ /////////////////////////
______(- 5)_____[- 2]_______[3]_____(6)_____
////////////////////////////////////////////////
ответ : x ∈ (- 5 ; - 2] ∪ [3 ; 6)
Объяснение:
Вопрос 1.
Такую функцию называют обратимой.
Обратимой называется функция в которой произвольному значению функции соответствует единственное значение аргумента.
Вопрос 2.
Исходная обратимая функция и функция, полученная из нее путем замены x на y и y на x, называются обратными.
у=5х+2
х=5у+2
5у=х-2
у=0,2(х-2)
Вопрос 3.
Строго монотонная функция обратима.
Да, является.
Вопрос 4.
Обратимые функции:
у=5х+2
у=х⁵
у=х³+1
Если найти производную каждой фцнкции, то выяснится, что функции монотонны, а заначит обратимы.
27х^2=3
9x^2=1
9x^2-1=0
Раскладываем левую часть по формуле разности квадратов:
(3х-1)(3х+1)=0
Приравниваем каждый множитель к нулю:
3х-1=0 3х+1=0
3х=1 3х= -1
х=1/3 х= -(1/3)
ответ: х1= 1/3, х2= -1/3