Представим левую часть уравнения в виде:
![\dfrac{(\sqrt[3]{2-x}+\sqrt[3]{7+x})(\sqrt[3]{(2-x)^2}+\sqrt[3]{(7+x)^3}-\sqrt[3]{(7+x)(2-x)})}{\sqrt[3]{2-x}+\sqrt[3]{7+x}}=3](/tpl/images/0491/8781/80ff6.png)
В числителе замечаем формулу суммы кубов
![\dfrac{(\sqrt[3]{2-x})^3+(\sqrt[3]{7+x})^3}{\sqrt[3]{2-x}+\sqrt[3]{7+x}}=3~~\Rightarrow~~ 2-x+7+x=3(\sqrt[3]{2-x}+\sqrt[3]{7+x})\\ \\ \sqrt[3]{2-x}+\sqrt[3]{7+x}=3](/tpl/images/0491/8781/f74af.png)
Пусть теперь ![\sqrt[3]{7+x}=a;~~\sqrt[3]{2-x}=b](/tpl/images/0491/8781/fccb6.png) , тогда, возведя до куба обе части равенства, мы имеем
, тогда, возведя до куба обе части равенства, мы имеем 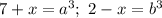 , получим
, получим
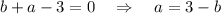 также
также 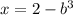 , подставляем в уравнение
, подставляем в уравнение 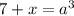
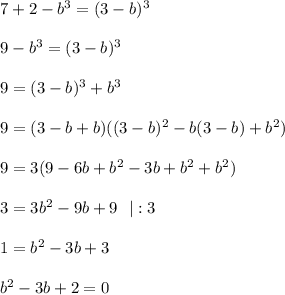
По теореме Виета
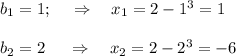
ответ: -6; 1.
Объяснение:
Функция - есть отношение или зависимость одной величины от другой по определённому закону, который и прописан в самой формуле функции.
Выражение y=f(x) расшифровывается как "Переменная у зависит от переменной х по формуле (закону) f.
Для того, чтобы правильно построить график какой-либо функции, вам необходимо понимать (видеть) общие для множества функций признаки.
К примеру, видеть, линейная это функция или квадратичная, экспоненциальная; периодическая, непрерывная и т.д. Все эти слова не должны быть для вас пустым звуком.
Если вы хотите правильно построить график, нужно начинать с области определения функции, т.е. определить, какие значения может принимать х, чтобы выражение имело решение. К примеру у=(1/х) - в таком выражении х не может быть равным 0, соответственно в точке х=0 - будет разрыв графика функции.
Я не могу здесь описывать весь раздел математики по всем видам функций, но вы должны следовать такому алгоритму при построении:
1) упростить выражение, если это возможно;
2) определить тип функции;
3) найти область определения функции;
4) в зависимости пунктов 2) и 3) найти координаты от 2 (для линейной функции) до 10 (для всех других) точек функции методом поочередного вычисления значения у для конкретного значения х, взятых с определенным вами же промежутком приращения;
5) построить и соединить полученные точки линиями (отрезками или кривыми) в зависимости от пунктов 2) и 3).
Если вы ничего не поняли из вышеописанного, а график строить надо, просто вычислите 10 координат точек графика функции, начиная с
х = -5 и заканчивая
х = 5 с приращением 0,5 каждую новую точку.
пример: функция у=х²-1
подставляем
х = -5, получаем у = 24
х= -4,5 получаем у= 19,25
х= -4 получаем у= 15 ...
.. и так далее до х=5.
В результате получим классическую параболу, сдвинутую вдоль оси ординат (у) вниз на 1 единицу.
Надеюсь, мой труд не пропал зря.
ответ: x=1
Объяснение:
ОДЗ: x>=0
Замена:√x=t>=0 (тк квадратный корень не отрицателен)
t+t^6=3-t^2
t^6+t^2+t-3=0
(t^6-1) +(t^2-1) +(t-1)=0
t^6-1= (t^2)^3 -1^3 = (t^2-1)* (t^4+t^2+1)= (t-1)* (t+1)*(t^4+t^2+1)=
(t-1)*(t^5+t^4+t^3+t^2+t+1) (то же самое можно получить по общей формуле разности степеней ,если вам она известна : a^n-b^n)
(t-1)* (t^5+t^4+t^3+t^2+t+1) +(t-1)*(t+1) +(t-1)=0
(t-1)* (t^5+t^4+t^3+t^2+2t+3)=0
Как было оговорено ранее: √x=t>=0
Тогда все одночлены в многочлене:
t^5+t^4+t^3+t^2+2t+3
неотрицательны, а свободный член 3 cтрого положителен.
Сумма неотрицательных членов и положительного члена положительна:
t^5+t^4+t^3+t^2+2t+3 >0
Вывод: t^5+t^4+t^3+t^2+2t+3=0 (не имеет решений)
Таким образом уравнение:
(t-1)* (t^5+t^4+t^3+t^2+2t+3)=0
имеет единственное решение : t=1
√x=1
x=1
ответ: x=1
Стандартное уравнение. Для упрощения можно сделать замену.
Заметим, что
Формула сокращённого умножения --- сумма кубов
Или можно было домножить обе части на (а + b), при этом заметив формулу.
Получаем, что
На этом этапе можно возвести обе части в куб, применим формулу куба суммы:
По теореме, обратной т. Виета, находим корни:
Первый корень --- - 6
Второй корень --- 1
Проверкой убеждаемся, что оба корня подходят.
ОТВЕТ: - 6 ; 1