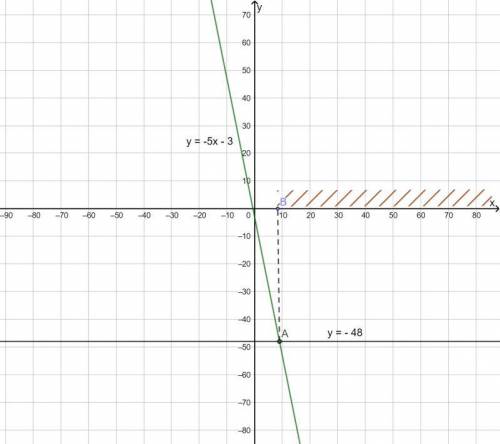
1) При x ≥ 9 значения функции y = -5x - 3 не больше -48.
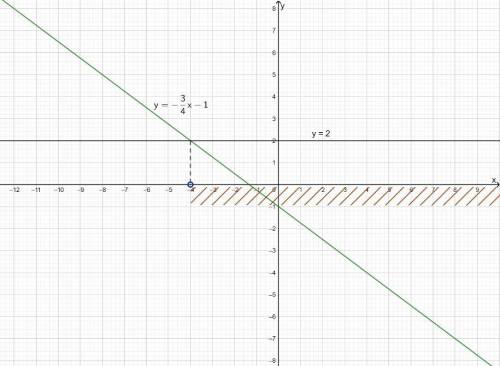
2) При x > -4 значения функции y = -3/4 *x - 1 меньше 2.
Объяснение:
Рисунки прилагаются.
1) y = -5x - 3 линейная функция, график прямая линия, пересекает ось OY в точке (0; --3).
Выберем еще одну точку и построим график функции: x = 10; y = -50-3 = -53.
При каких значениях x значения функции не больше (значит меньше или равно) -48?
Построим в этой же системе координат прямую y = -48.
По графикам видно, что что -5x - 3 ≤ -48 при x ≥ 9
Проверим аналитически:
-5x -3 ≤ -48; -5x ≤ -48 +3; -5x ≤ -45; x ≥ 9.
2) y = -3/4*x - 3 = -0,75x - 1 линейная функция, график прямая линия, пересекает ось OY в точке (0; -1).
Выберем еще одну точку и построим график функции: x = 4;
y = -0,75*4 -1 = -3 - 1 = -4.
При каких значениях x значения функции меньше 2?
Построим в этой же системе координат прямую y = 2.
По графикам видно, что -0,75x - 1 ≤ -2 при x > -4
Проверим аналитически:
-0,75x -1 < 2; -0,75x < 3; x > -4.
x = - 34
Объяснение:
Если в скобках стоит дробь, то так:
cos ((10x-48)*Π/(3x+5)) = 1
Это табличное значение, cos(2Π*n) = 1
(10x-48)*Π/(3x+5) = 2Π*n, n € Z
Делим все на П
(10x-48)/(3x+5) = 2n
Область определения: x ≠ -5/3
10x-48 = 2(3x+5)*n
Делим все на 2
5x-24 = 3nx + 5n
x(5-3n) = 24+5n
x = (5n+24)/(5-3n), n € Z
При четных n числитель четный, а знаменатель нет.
При нечетных n знаменатель четный, а числитель нет.
В обоих случаях дробь будет нецелой.
Единственный целый корень будет, если знаменатель равен 1 или -1.
5-3n = 1; 5-1 = 3n = 4;
n = 4/3 не подходит.
5-3n = -1; 5+1 = 3n = 6; n = 2;
x = (10+24)/(5-6) = -34
Данное уравнение 3x^2-19x+21=0 является неприведённым квадратным уравнением вида:
ax^2+bx+c=0 по теореме Виета следует:
х1*х2=с/а
Отсюда произведение корней данного уравнения равно:
х1*х2=21/3=7
ответ: Произведение корней данного уравнения равно 7