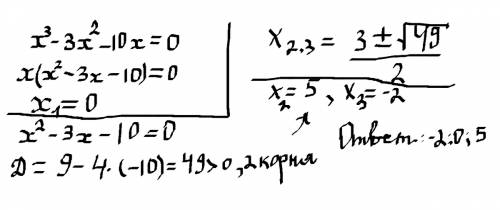
Xn= 8 n-4
Xn= 4*3
Объяснение:
Последовательности можно задавать различными среди которых особенно важны три: аналитический, словесный и рекуррентный. В этой задаче рассмотрим два задания последовательности:
рекуррентное задание последовательности:
это такой задания последовательности, при котором указывают правило, позволяющее вычислить n-й член последовательности, если известны её предыдущие члены.
Аналитическое задание последовательности:
говорят, что последовательность задана аналитически, если указана формула её n-го члена yn=f(n).
1. Рассмотрим заданную рекуррентным последовательность x1=4,xn=xn−1+8, n=2,3,4...
n-й член последовательности получается из предыдущего (n−1)-го члена прибавлением к нему числа 8.
Тем самым получаем последовательность:
4; 12; 20; 28...
Для того чтобы последовательность можно было задать аналитически, преобразуем выражение:
xn=4+8(n−1)=8n−4.
Итак, мы получили формулу n-го члена заданной последовательности:
xn=8n−4.
2. Рассмотрим вторую, заданную рекуррентным последовательность x1=4,xn=3xn−1, n=2,3,4...
n-й член последовательности получается из предыдущего (n−1)-го члена умножением его на 3.
Тем самым получаем последовательность:
4; 12; 36; 108...
И формула n-го члена заданной последовательности:
xn=4⋅3n−1.
Периметр прямоугольника равен 64 см , значит полупериметр равен 32 см . Обозначим длину прямоугольника через a , тогда его ширина равна (32 - a) , а значит его площадь равна : a * (32 - a) .
Одну его сторону увеличили на 2 см , она стала равна (a + 2) . Другую сторону уменьшили на 4 см, она стала равна (32 - a - 4) = (28 - a) .
Значит теперь площадь этого прямоугольника равна :
(a + 2)*(28 - a) , что по условию задачи на 4 см² меньше площади исходного прямоугольника. Составим и решим уравнение:
a * (32 - a) = (a + 2)(28 - a)
32a - a² = 28a - a² + 56 - 2a
32a - a² - 26a = 56
6a = 56
a= 9 1/3 см - длина исходного прямоугольника
32 - 9 1/3 = 22 2/3 см - ширина исходного прямоугольника